Решение определенного интеграла по частям. Интегрирование по частям
Функция F(x), дифференцируемая в данном промежутке X, называется первообразной для функции f(x), или интегралом от f(x), если для всякого x ∈X справедливо равенство:
F " (x) = f(x). (8.1)
Нахождение всех первообразных для данной функции называется ее интегрированием. Неопределенным интегралом функции f(x) на данном промежутке Х называется множество всех первообразных функций для функции f(x); обозначение -
Если F(x) - какая-нибудь первобразная для функции f(x), то ∫ f(x)dx = F(x) + C, (8.2)
где С- произвольная постоянная.
Таблица интегралов
Непосредственно из определения получаем основные свойства неопределенного интеграла и список табличных интегралов:
1) d∫f(x)dx=f(x)
2)∫df(x)=f(x)+C
3) ∫af(x)dx=a∫f(x)dx (a=const)
4) ∫(f(x)+g(x))dx = ∫f(x)dx+∫g(x)dx
Список табличных интегралов
1. ∫x m dx = x m+1 /(m + 1) +C; (m ≠ -1)
3.∫a x dx = a x /ln a + C (a>0, a ≠1)
4.∫e x dx = e x + C
5.∫sin x dx = cosx + C
6.∫cos x dx = - sin x + C
7. = arctg x + C
8. = arcsin x + C
10. = - ctg x + C
Замена переменной
Для интегрирования многих функций применяют метод замены переменной или подстановки, позволяющий приводить интегралы к табличной форме.
Если функция f(z) непрерывна на [α,β], функция z =g(x) имеет на непрерывную производную и α ≤ g(x) ≤ β, то
∫ f(g(x)) g " (x) dx = ∫f(z)dz, (8.3)
причем после интегрирования в правой части следует сделать подстановку z=g(x).
Для доказательства достаточно записать исходный интеграл в виде:
∫ f(g(x)) g " (x) dx = ∫ f(g(x)) dg(x).
Например:
Метод интегрирования по частям
Пусть u = f(x) и v = g(x) - функции, имеющие непрерывные . Тогда, по произведения,
d(uv))= udv + vdu или udv = d(uv) - vdu.
Для выражения d(uv) первообразной, очевидно, будет uv, поэтому имеет место формула:
∫ udv = uv - ∫ vdu (8.4.)
Эта формула выражает правило интегрирования по частям . Оно приводит интегрирование выражения udv=uv"dx к интегрированию выражения vdu=vu"dx.
Пусть, например, требуется найти ∫xcosx dx. Положим u = x, dv = cosxdx, так что du=dx, v=sinx. Тогда
∫xcosxdx = ∫x d(sin x) = x sin x - ∫sin x dx = x sin x + cosx + C.
Правило интегрирования по частям имеет более ограниченную область применения, чем замена переменной. Но есть целые классы интегралов, например,
∫x k ln m xdx, ∫x k sinbxdx, ∫ x k cosbxdx, ∫x k e ax и другие, которые вычисляются именно с помощью интегрирования по частям.
Определенный интеграл
Понятие определенного интеграла вводится следующим образом. Пусть на отрезке определена функция f(x). Разобьем отрезок [
a,b] на n
частей точками a= x 0 < x 1 <...< x n = b. Из каждого интервала (x i-1 ,
x i) возьмем произвольную точку ξ i и составим сумму f(ξ i)
Δx i где
Δ
x i =x i - x i-1
. Сумма вида f(ξ i)Δ
x i называется интегральной суммой
, а ее предел при λ = maxΔx i → 0, если он существует и конечен, называется определенным интегралом
функции f(x) от a
до b
и обозначается:
F(ξ i)Δx i (8.5).
Функция f(x) в этом случае называется интегрируемой на отрезке , числа a и b носят название нижнего и верхнего предела интеграла .
Для определенного интеграла справедливы следующие свойства:
4), (k = const, k∈R);
5)
6)
7) f(ξ)(b-a) (ξ∈).
Последнее свойство называется теоремой о среднем значении .
Пусть f(x) непрерывна на . Тогда на этом отрезке существует неопределенный интеграл
∫f(x)dx = F(x) + C
и имеет место формула Ньютона-Лейбница , cвязывающая определенный интеграл с неопределенным:
F(b) - F(a). (8.6)
Геометрическая интерпретация: определенный интеграл представляет собой площадь криволинейной трапеции, ограниченной сверху кривой y=f(x), прямыми x = a и x = b и отрезком оси Ox .
Несобственные интегралы
Интегралы с бесконечными пределами и интегралы от разрывных (неограниченных) функций называются несобственными. Несобственные интегралы I рода - это интегралы на бесконечном промежутке, определяемые следующим образом:
(8.7)
Если этот предел существует и конечен, то называется сходящимся несобственным интегралом от f(x) на интервале [а,+ ∞), а функцию f(x) называют интегрируемой на бесконечном промежутке [а,+ ∞). В противном случае про интеграл говорят, что он не существует или расходится .
Аналогично определяются несобственные интегралы на интервалах (-∞,b] и (-∞, + ∞):
Определим понятие интеграла от неограниченной функции. Если f(x) непрерывна для всех значений x отрезка , кроме точки с, в которой f(x) имеет бесконечный разрыв, то несобственным интегралом II рода от f(x) в пределах от a до b называется сумма:
если эти пределы существуют и конечны. Обозначение:
Примеры вычисления интегралов
Пример 3.30. Вычислить ∫dx/(x+2).
Решение. Обозначим t = x+2, тогда dx = dt, ∫dx/(x+2) = ∫dt/t = ln|t| + C = ln|x+2| + C .
Пример 3.31 . Найти ∫ tgxdx.
Решение. ∫ tgxdx = ∫sinx/cosxdx = - ∫dcosx/cosx. Пусть t=cosx, тогда ∫ tgxdx = -∫ dt/t = - ln|t| + C = -ln|cosx|+C.
Пример 3.32 . Найти ∫dx/sinxРешение.
Пример 3.33. Найти .
Решение. = .
Пример 3.34 . Найти ∫arctgxdx.
Решение. Интегрируем по частям. Обозначим u=arctgx, dv=dx. Тогда
du = dx/(x 2 +1), v=x, откуда ∫arctgxdx = xarctgx - ∫ xdx/(x 2 +1) = xarctgx + 1/2 ln(x 2 +1) +C; так как
∫xdx/(x 2 +1) = 1/2 ∫d(x 2 +1)/(x 2 +1) = 1/2 ln(x 2 +1) +C.
Пример 3.35 . Вычислить ∫lnxdx.
Решение.
Применяя формулу интегрирования по частям, получим:
u=lnx, dv=dx, du=1/x dx, v=x. Тогда ∫lnxdx = xlnx - ∫x 1/x dx =
= xlnx - ∫dx + C= xlnx - x + C.
Пример 3.36 . Вычислить ∫e x sinxdx.
Решение.
Обозначим u = e x , dv = sinxdx, тогда du = e x dx, v =∫sinxdx= - cosx → ∫ e x sinxdx = - e x cosx + ∫ e x cosxdx. Интеграл
∫e x cosxdx также интегрируем по частям: u = e x , dv = cosxdx,
du=e x dx, v=sinx. Имеем:
∫ e x cosxdx = e x sinx - ∫ e x sinxdx. Получили соотношение
∫e x sinxdx = - e x cosx + e x sinx - ∫ e x sinxdx, откуда 2∫e x sinx
dx = - e x cosx + e x sinx + С.
Пример 3.37. Вычислить J = ∫cos(lnx)dx/x.
Решение. Так как dx/x = dlnx, то J= ∫cos(lnx)d(lnx). Заменяя lnx через t, приходим к табличному интегралу J = ∫ costdt = sint + C = sin(lnx) + C.
Пример 3.38 . Вычислить J = .
Решение.
Учитывая, что = d(lnx), производим подстановку lnx = t. Тогда J = 
.
Пример
3.39
. Вычислить интеграл J = 
.
Решение.
Имеем: 
. Поэтому =
=
=.
вводится так sqrt(tan(x/2)).
А если в окне результата нажмете на Show steps в правом верхнем углу, то получите подробное решение.
Метод интегрирования по частям применяется, в основном, когда подынтегральная функция состоит из произведения двух сомножителей определенного вида. Формула интегрирования по частям имеет вид:
Она
дает возможность свести вычисление
заданного интеграла
к вычислению интеграла
,
который оказывается более простым, чем
данный.
Большую часть интегралов, вычисляемых методом интегрирования по частям, можно разбить на три группы:
1.
Интегралы вида
,
,
,
где
– многочлен,
– число, не равное нулю
В
этом случае через
обозначают многочлен
.
2.
Интегралы вида
,
,
,
,
,
где
– многочлен.
В
этом случае через
обозначают
,
а всю остальную часть подынтегрального
выражения через
:
3.
Интегралы вида
,
,
где
– числа.
В
этом случае через
обозначают
и применяют формулу интегрирования по
частям дважды, возвращаясь в результате
к исходному интегралу, после чего
исходный интеграл выражается из
равенства.
Замечание : В некоторых случаях для нахождения заданного интеграла формулу интегрирования по частям необходимо применять несколько раз. Также метод интегрирования по частям комбинируют с другими методами.
Пример 26.
Найти
интегралы методом по частям: а)
;
б)
.
Решение.
б)
3.1.4. Интегрирование дробно-рациональных функций
Дробно-рациональной
функцией
(рациональной
дробью) называется функция, равная
отношению двух многочленов:
,
где
– многочлен степени
,
– многочлен степени
.
Рациональная
дробь называется
правильной
,
если степень многочлена в числителе
меньше степени многочлена в знаменателе,
т.е.
,
в противном случае (если
)
рациональная дробь называется
неправильной
.
Любую
неправильную рациональную дробь можно
представить в виде суммы многочлена
и правильной рациональной дроби, разделив
числитель на знаменатель по правилу
деления многочленов:
,
где
– целая часть от деления,
– правильная рациональная дробь,
– остаток от деления.
Правильные рациональные дроби вида:
I.
;
II.
;
III.
;
IV.
,
где
,
,
,
,
,
,
– действительные
числа и
(т.е. квадратный трехчлен в знаменателеIII и IV
дробей не имеет корней – дискриминант
отрицательный) называются
простейшими
рациональными дробями
I, II, III и IV типов
.
Интегрирование простейших дробей
Интегралы от простейших дробей четырех типов вычисляются следующим образом.
I)
.
II)
,
.
III)
Для интегрирования простейшей дроби
III типа в знаменателе выделяют полный
квадрат, производят замену
.
Интеграл после подстановки разбивают
на два интеграла. Первый интеграл
вычисляют выделением в числителе
производной знаменателя, что дает
табличный интеграл, а второй интеграл
преобразовывают к виду
,
так как
,
что также дает табличный интеграл.
;
IV)
Для
интегрирования простейшей дроби IV типа
в знаменателе выделяют полный квадрат,
производят замену
.
Интеграл после подстановки разбивают
на два интеграла. Первый интеграл
вычисляют подстановкой
,
а второй с помощью рекуррентных
соотношений.
Пример 27.
Найти интегралы от простейших дробей:
а)
;
б)
;
в)
.
Решение.
а)
.
Всякую правильную рациональную дробь, знаменатель которой может быть разложен на множители, можно представить в виде суммы простейших дробей. Разложение на сумму простейших дробей осуществляют методом неопределенных коэффициентов. Он заключается в следующем:
соответствует одна дробь вида
;
–
каждому
множителю знаменателя
соответствует сумма
дробей
вида
соответствует дробь вида
;
– каждому
квадратному множителю знаменателя
соответствует сумма
дробей вида
где – неопределенные коэффициенты.
Для нахождения неопределенных коэффициентов правую часть в виде суммы простейших дробей приводят к общему знаменателю и преобразовывают. В результате получается дробь с тем же знаменателем, что и в левой части равенства. Затем отбрасывают знаменатели и приравнивают числители. В результате получается тождественное равенство, в котором левая часть – многочлен с известными коэффициентами, а правая часть – многочлен с неопределенными коэффициентами.
Существует два способа определения неизвестных коэффициентов: метод неопределенных коэффициентов и метод частных значений.
Метод неопределенных коэффициентов.
Т.к.
многочлены тождественно равны, то равны
коэффициенты при одинаковых степенях
.
Приравнивая коэффициенты при одинаковых
степенях
в многочленах левой и правой частей,
получим систему линейных уравнений.
Решая систему, определяем неопределенные
коэффициенты.
Метод частных значений.
Т.к.
многочлены тождественно равны, то,
подставляя вместо
в левую и правую части любое число,
получим верное равенство, линейное
относительно неизвестных коэффициентов.
Подставляя столько значений
,
сколько неизвестных коэффициентов,
получим систему линейных уравнений.
Вместо
в левую и правую части можно подставлять
любые числа, однако более удобно
подставлять корни знаменателей дробей.
После нахождения значений неизвестных коэффициентов, исходная дробь записывается в виде суммы простейших дробей в подынтегральное выражение и осуществляется ранее рассмотренное интегрирование по каждой простейшей дроби.
Схема интегрирования рациональных дробей:
1. Если подынтегральная дробь неправильная, то необходимо представить ее в виде суммы многочлена и правильной рациональной дроби (т.е. разделить многочлен числителя на многочлен знаменателя с остатком). Если подынтегральная дробь правильная сразу переходим ко второму пункту схемы.
2. Разложить знаменатель правильной рациональной дроби на множители, если это возможно.
3. Разложить правильную рациональную дробь на сумму простейших рациональных дробей, используя метод неопределенных коэффициентов.
4. Проинтегрировать полученную сумму многочлена и простейших дробей.
Пример 28.
Найти интегралы от рациональных дробей:
а)
;
б)
;
в)
.
Решение.
а)
.
Т.к. подынтегральная функция неправильная рациональная дробь, то выделим целую часть, т.е. представим ее в виде суммы многочлена и правильной рациональной дроби. Разделим многочлен в числителе на многочлен в знаменателе уголком.
Исходный
интеграл примет вид:
.
Разложим правильную рациональную дробь на сумму простейших дробей c помощью метода неопределенных коэффициентов:
,
получаем:
Решая систему линейных уравнений, получим значения неопределенных коэффициентов: А = 1; В = 3.
Тогда
искомое разложение имеет вид:
.
=
.
б)
.
.
Отбросим знаменатели и приравняем левую и правую части:
Приравнивая
коэффициенты при одинаковых степенях
,
получаем систему:
Решая систему из пяти линейных уравнений, находим неопределенные коэффициенты:
.
Найдем исходный интеграл, учитывая полученное разложение:
.
в)
.
Разложим подынтегральную функцию (правильную рациональную дробь) на сумму простейших дробей с помощью метода неопределенных коэффициентов. Разложение ищем в виде:
.
Приведя к общему знаменателю, получим:
Отбросим знаменатели и приравняем левую и правую части:
Для
нахождения неопределенных коэффициентов
применим метод частных значений. Придадим
частные
значения
,
при которых множители обращаются в
нуль, т. е. подставим эти значения в
последнее выражение и получим три
уравнения:
; 
;
; 
;
; 
.
Тогда искомое разложение имеет вид:
Найдем исходный интеграл, учитывая полученное разложение:
Интегрирование по частям. Примеры решений
И снова, здравствуйте. Сегодня на уроке мы научимся интегрировать по частям. Метод интегрирования по частям – это один из краеугольных камней интегрального исчисления. На зачете, экзамене студенту почти всегда предлагают решить интегралы следующих типов: простейший интеграл (см. статью ) либо интеграл на замену переменной (см. статью ) либо интеграл как раз на метод интегрирования по частям .
Как всегда, под рукой должны быть: Таблица интегралов и Таблица производных . Если у Вас до сих пор их нет, то, пожалуйста, посетите кладовку моего сайта: Математические формулы и таблицы . Не устану повторять – лучше всё распечатать. Весь материал я постараюсь изложить последовательно, просто и доступно, в интегрировании по частям нет особых трудностей.
Какую задачу решает метод интегрирования по частям? Метод интегрирования по частям решает очень важную задачу, он позволяет интегрировать некоторые функции, отсутствующие в таблице, произведение
функций, а в ряде случаев – и частное. Как мы помним, нет удобной формулы:
. Зато есть такая: 
– формула интегрирования по частям собственной персоной. Знаю, знаю, ты одна такая – с ней мы и будем работать весь урок (уже легче).
И сразу список в студию. По частям берутся интегралы следующих видов:
1) , 
, – логарифм, логарифм, умноженный на какой-нибудь многочлен.
2) ,
– экспоненциальная функция, умноженная на какой-нибудь многочлен. Сюда же можно отнести интегралы вроде – показательная функция, умноженная на многочлен, но на практике процентах так в 97, под интегралом красуется симпатичная буква «е». … что-то лирической получается статья, ах да… весна же пришла.
3) , 
, – тригонометрические функции, умноженные на какой-нибудь многочлен.
4) , – обратные тригонометрические функции («арки»), «арки», умноженные на какой-нибудь многочлен.
Также по частям берутся некоторые дроби, соответствующие примеры мы тоже подробно рассмотрим.
Интегралы от логарифмов
Пример 1
Классика. Время от времени данный интеграл можно встретить в таблицах, но пользоваться готовым ответом нежелательно, так как у преподавателя весенний авитаминоз и он сильно заругается. Потому что рассматриваемый интеграл отнюдь не табличный – он берётся по частям. Решаем:
Прерываем решение на промежуточные объяснения.
Используем формулу интегрирования по частям: 
Формула применяется слева направо
Смотрим на левую часть: . Очевидно, что в нашем примере (и во всех остальных, которые мы рассмотрим) что-то нужно обозначить за , а что-то за .
В интегралах рассматриваемого типа за всегда обозначается логарифм.
Технически оформление решения реализуется следующим образом, в столбик записываем:
То есть, за мы обозначили логарифм, а за – оставшуюся часть подынтегрального выражения.
Следующий этап: находим дифференциал :
Дифференциал – это почти то же самое, что и производная, как его находить, мы уже разбирали на предыдущих уроках.
Теперь находим функцию . Для того чтобы найти функцию необходимо проинтегрировать правую часть нижнего равенства :
Теперь открываем наше решение и конструируем правую часть формулы: .
Вот кстати, и образец чистового решения с небольшими пометками:
Единственный момент, в произведении я сразу переставил местами и , так как множитель принято записывать перед логарифмом.
Как видите, применение формулы интегрирования по частям, по сути дела, свело наше решение к двум простым интегралам.
Обратите внимание, что в ряде случаев сразу после применения формулы, под оставшимся интегралом обязательно проводится упрощение – в рассматриваемом примере мы сократили подынтегральное выражение на «икс».
Выполним проверку. Для этого нужно взять производную от ответа:
Получена исходная подынтегральная функция, значит, интеграл решён правильно.
В ходе проверки мы использовали правило дифференцирования произведения: 
. И это не случайно.
Формула интегрирования по частям 
и формула 
– это два взаимно обратных правила.
Пример 2
Найти неопределенный интеграл.
Подынтегральная функция представляет собой произведение логарифма на многочлен.
Решаем.
Я еще один раз подробно распишу порядок применения правила, в дальнейшем примеры будут оформляться более кратко, и, если у Вас возникнут трудности в самостоятельном решении, нужно вернуться обратно к первым двум примерам урока.
Как уже говорилось, за необходимо обозначить логарифм (то, что он в степени – значения не имеет). За обозначаем оставшуюся часть подынтегрального выражения.
Записываем в столбик:
Сначала находим дифференциал :
Здесь использовано правило дифференцирования сложной функции 
. Не случайно, на самом первом уроке темы Неопределенный интеграл. Примеры решений
я акцентировал внимание на том, что для того, чтобы освоить интегралы, необходимо «набить руку» на производных. С производными придется столкнуться еще не раз.
Теперь находим функцию , для этого интегрируем правую часть нижнего равенства :
Для интегрирования мы применили простейшую табличную формулу 
Теперь всё готово для применения формулы 
. Открываем «звёздочкой» и «конструируем» решение в соответствии с правой частью :
Под интегралом у нас снова многочлен на логарифм! Поэтому решение опять прерывается и правило интегрирования по частям применяется второй раз. Не забываем, что за в похожих ситуациях всегда обозначается логарифм.
Хорошо бы, если к данному моменту простейшие интегралы и производные Вы умели находить устно.
(1) Не путаемся в знаках! Очень часто здесь теряют минус, также обратите внимание, что минус относится ко всей
скобке 
, и эти скобки нужно корректно раскрыть.
(2) Раскрываем скобки. Последний интеграл упрощаем.
(3) Берем последний интеграл.
(4) «Причесываем» ответ.
Необходимость дважды (а то и трижды) применять правило интегрирования по частям возникает не так уж и редко.
А сейчас пара примеров для самостоятельного решения:
Пример 3
Найти неопределенный интеграл.
Этот пример решается методом замены переменной (или подведением под знак дифференциала)! А почему бы и нет – можете попробовать взять его по частям, получится забавная вещь.
Пример 4
Найти неопределенный интеграл.
А вот этот интеграл интегрируется по частям (обещанная дробь).
Это примеры для самостоятельного решения, решения и ответы в конце урока.
Вроде бы в примерах 3,4 подынтегральные функции похожи, а вот методы решения – разные! В этом-то и состоит основная трудность освоения интегралов – если неправильно подобрать метод решения интеграла, то возиться с ним можно часами, как с самой настоящей головоломкой. Поэтому чем больше вы прорешаете различных интегралов – тем лучше, тем легче пройдут зачет и экзамен. Кроме того, на втором курсе будут дифференциальные уравнения, а без опыта решения интегралов и производных делать там нечего.
По логарифмам, пожалуй, более чем достаточно. На закуску могу еще вспомнить, что студенты-технари логарифмами называют женскую грудь =). Кстати, полезно знать назубок графики основных элементарных функций: синуса, косинуса, арктангенса, экспоненты, многочленов третьей, четвертой степени и т.д. Нет, конечно, презерватив на глобус
я натягивать не буду, но теперь вы многое запомните из раздела Графики и функции
=).
Интегралы от экспоненты, умноженной на многочлен
Общее правило:
Пример 5
Найти неопределенный интеграл.
Используя знакомый алгоритм, интегрируем по частям:
Если возникли трудности с интегралом , то следует вернуться к статье Метод замены переменной в неопределенном интеграле .
Единственное, что еще можно сделать, это «причесать» ответ:
Но если Ваша техника вычислений не очень хороша, то самый выгодный вариант оставить ответом 
или даже 
То есть, пример считается решенным, когда взят последний интеграл. Ошибкой не будет, другое дело, что преподаватель может попросить упростить ответ.
Пример 6
Найти неопределенный интеграл.
Это пример для самостоятельного решения. Данный интеграл дважды интегрируется по частям. Особое внимание следует обратить на знаки – здесь легко в них запутаться, также помним, что – сложная функция.
Больше про экспоненту рассказывать особо нечего. Могу только добавить, что экспонента и натуральный логарифм взаимно-обратные функции, это я к теме занимательных графиков высшей математики =) Стоп-стоп, не волнуемся, лектор трезв.
Интегралы от тригонометрических функций, умноженных на многочлен
Общее правило: за всегда обозначается многочлен
Пример 7
Найти неопределенный интеграл.
Интегрируем по частям:
Хммм, …и комментировать нечего.
Пример 8
Найти неопределенный интеграл
Это пример для самостоятельного решения
Пример 9
Найти неопределенный интеграл
Еще один пример с дробью. Как и в двух предыдущих примерах за обозначается многочлен.
Интегрируем по частям:
Если возникли трудности или недопонимание с нахождением интеграла , то рекомендую посетить урок Интегралы от тригонометрических функций .
Пример 10
Найти неопределенный интеграл
Это пример для самостоятельного решения.
Подсказка: перед использованием метода интегрирования по частям следует применить некоторую тригонометрическую формулу, которая превращает произведение двух тригонометрических функций в одну функцию. Формулу также можно использовать и в ходе применения метода интегрирования по частям, кому как удобнее.
Вот, пожалуй, и всё в данном параграфе. Почему-то вспомнилась строчка из гимна физмата «А синуса график волна за волной по оси абсцисс пробегает»….
Интегралы от обратных тригонометрических функций.
Интегралы от обратных тригонометрических функций, умноженных на многочлен
Общее правило: за всегда обозначается обратная тригонометрическая функция .
Напоминаю, что к обратным тригонометрическим функциям относятся арксинус, арккосинус, арктангенс и арккотангенс. Для краткости записи я буду называть их «арками»
В этой теме мы подробно поговорим вычислении неопределённых интегралов с помощью так называемой "формулы интегрирования по частям". Нам понадобится таблица неопределенных интегралов и таблица производных . В первой части будут разобраны стандартные примеры, которые большей частью встречаются в типовых расчётах и контрольных работах. Более сложные примеры разобраны во второй части .
Постановка задачи в стандартном случае следующая. Допустим, под интегралом у нас расположены две функции разной природы : многочлен и тригонометрическая функция, многочлен и логарифм, многочлен и обратная тригонометрическая функция и так далее. В этой ситуации выгодно отделить одну функцию от другой. Грубо говоря, имеет смысл разбить подынтегральное выражение на части, - и разобраться с каждой частью по отдельности. Отсюда и название: "интегрирование по частям". Применение этого метода основано на следующей теореме:
Пусть функции $u(x)$ и $v(x)$ дифференцируемы на некотором промежутке, и на этом промежутке существует интеграл $\int v \; du$. Тогда на этом же промежутке существует и интеграл $\int u \; dv$, при этом верно следущее равенство:
\begin{equation} \int u \; dv=u\cdot v-\int v\; du \end{equation}
Формулу (1) и называют "формулой интегрирования по частям". Иногда, применяя вышеуказанную теорему, говорят о использовании "метода интегрирования по частям". Нам будет важна суть этого метода, которую и рассмотрим на примерах. Существует несколько стандартных случаев, в которых явно применима формула (1). Именно эти случаи и станут темой данной страницы. Пусть $P_n(x)$ - многочлен n-й степени. Введём два правила:
Правило №1
Для интегралов вида $\int P_n(x) \ln x \;dx$, $\int P_n(x) \arcsin x \;dx$, $\int P_n(x) \arccos x \;dx$, $\int P_n(x)\arctg x \;dx$, $\int P_n(x) \arcctg x \;dx$ принимаем $dv=P_n(x)dx$.
Правило №2
Для интегралов вида $\int P_n(x) a^x \;dx$ ($a$ - некоторое положительное число), $\int P_n(x) \sin x \;dx$, $\int P_n(x) \cos x \;dx$, $\int P_n(x)ch x \;dx$, $\int P_n(x) sh x \;dx$ принимаем $u=P_n(x)$.
Сразу отмечу, что указанные выше записи не нужно воспринимать буквально. Например, в интегралах вида $\int P_n(x) \ln x \;dx$ не обязательно будет стоять именно $\ln x$. Там могут быть расположены и $\ln 5x$, и $\ln (10x^2+14x-5)$. Т.е. запись $\ln x$ нужно воспринимать как своего рода обобщение.
Ещё один момент. Бывает, что формулу интегрирования по частям приходится применять несколько раз. Об этом поговорим подробнее в примерах №4 и №5. Теперь перейдём непосредственно к решению типичных задач. Решение задач, уровень которых чуть выше стандартных, разбирается во второй части .
Пример №1
Найти $\int (3x+4) \cos (2x-1) \; dx$.
Под интегралом расположен многочлен $3x+4$ и тригонометрическая функция $\cos (2x-1)$. Это классический случай для применения формулы , поэтому возьмём заданный интеграл по частям. Формула требует, чтобы интеграл $\int (3x+4) \cos (2x-1) \; dx$ был представлен в форме $\int u \; dv$. Нам нужно выбрать выражения для $u$ и для $dv$. Можно в качестве $u$ принять $3x+4$, тогда $dv=\cos (2x-1)dx$. Можно взять $u=\cos (2x-1)$, тогда $dv=(3x+4)dx$. Чтобы сделать правильный выбор обратимся к . Заданный интеграл $\int (3x+4) \cos (2x-1) \; dx$ подпадает под вид $\int P_n(x) \cos x \;dx$ (многочлен $P_n(x)$ в нашем интеграле имеет вид $3x+4$). Согласно нужно выбрать $u=P_n(x)$, т.е. в нашем случае $u=3x+4$. Так как $u=3x+4$, то $dv=\cos(2x-1)dx$.
Однако недостаточно просто выбрать $u$ и $dv$. Нам еще понадобятся значения $du$ и $v$. Так как $u=3x+4$, то:
$$ du=d(3x+4)=(3x+4)"dx=3dx.$$
Теперь разберёмся с функцией $v$. Так как $dv=\cos(2x-1)dx$, то согласно определению неопределённого интеграла имеем: $ v=\int \cos(2x-1)\; dx$. Чтобы найти нужный интеграл применим внесение под знак дифференциала :
$$ v=\int \cos(2x-1)\; dx=\frac{1}{2}\cdot \int \cos(2x-1)d(2x-1)=\frac{1}{2}\cdot \sin(2x-1)+C=\frac{\sin(2x-1)}{2}+C. $$
Однако нам нужно не всё бесконечное множество функций $v$, которое описывает формула $\frac{\sin(2x-1)}{2}+C$. Нам нужна какая-то одна функция из этого множества. Чтобы получить искомую функцию нужно вместо $C$ подставить какое-либо число. Проще всего, разумеется, подставить $C=0$, получив при этом $v=\frac{\sin(2x-1)}{2}$.
Итак, соберём всё вышеизложенное воедино. Мы имеем: $u=3x+4$, $du=3dx$, $dv=\cos(2x-1)dx$, $v=\frac{\sin(2x-1)}{2}$. Подставляя всё это в правую часть формулы будем иметь:
$$ \int (3x+4) \cos (2x-1) \; dx=(3x+4)\cdot\frac{\sin(2x-1)}{2}-\int \frac{\sin(2x-1)}{2}\cdot 3dx. $$
Осталось, по сути, только найти $\int\frac{\sin(2x-1)}{2}\cdot 3dx$. Вынося константу (т.е. $\frac{3}{2}$) за знак интеграла и применяя метод внесения под знак дифференциала , получим:
$$ (3x+4)\cdot \frac{\sin(2x-1)}{2}-\int \frac{\sin(2x-1)}{2}\cdot 3dx= \frac{(3x+4)\cdot\sin(2x-1)}{2}-\frac{3}{2}\int \sin(2x-1) \;dx= \\ =\frac{(3x+4)\cdot\sin(2x-1)}{2}-\frac{3}{4}\int \sin(2x-1) \;d(2x-1)= \frac{(3x+4)\cdot\sin(2x-1)}{2}-\frac{3}{4}\cdot (-\cos (2x-1))+C=\\ =\frac{(3x+4)\cdot\sin(2x-1)}{2}+\frac{3}{4}\cdot \cos (2x-1)+C. $$
Итак, $\int (3x+4) \cos (2x-1) \; dx=\frac{(3x+4)\cdot\sin(2x-1)}{2}+\frac{3}{4}\cdot \cos (2x-1)+C$. В сокращенном виде процесс решения записывают так:
$$ \int (3x+4) \cos (2x-1) \; dx=\left | \begin{aligned} & u=3x+4; \; du=3xdx.\\ & dv=\cos(2x-1)dx; \; v=\frac{\sin(2x-1)}{2}. \end{aligned} \right |=\\ =(3x+4)\cdot\frac{\sin(2x-1)}{2}-\int \frac{\sin(2x-1)}{2}\cdot 3dx= \frac{(3x+4)\cdot\sin(2x-1)}{2}-\frac{3}{2}\int \sin(2x-1) \;dx=\\ =\frac{(3x+4)\cdot\sin(2x-1)}{2}-\frac{3}{4}\cdot (-\cos (2x-1))+C= \frac{(3x+4)\cdot\sin(2x-1)}{2}+\frac{3}{4}\cdot \cos (2x-1)+C. $$
Неопределённый интеграл по частям найден, осталось лишь записать ответ.
Ответ : $\int (3x+4) \cos (2x-1) \; dx=\frac{(3x+4)\cdot\sin(2x-1)}{2}+\frac{3}{4}\cdot \cos (2x-1)+C$.
Полагаю, здесь не обойдётся без вопроса, поэтому попробую сформулировать его и дать ответ.
Почему мы приняли именно $u=3x+4$ и $dv=\cos(2x-1)dx$? Да, интеграл был решён. Но, может быть, если бы мы взяли $u=\cos (2x-1)$ и $dv=(3x+4)dx$ интеграл тоже был бы найден!
Нет, если принять $u=\cos (2x-1)$ и $dv=(3x+4)dx$, то ничего хорошего с этого не выйдет, - интеграл не упростится. Судите сами: если $u=\cos(2x-1)$, то $du=(\cos(2x-1))"dx=-2\sin(2x-1)dx$. Кроме того, так как $dv=(3x+4)dx$, то:
$$ v=\int (3x+4) \; dx=\frac{3x^2}{2}+4x+C.$$
Приняв $C=0$, получим $v=\frac{3x^2}{2}+4x$. Подставим теперь в формулу найденные значения $u$, $du$, $v$ и $dv$:
$$ \int (3x+4) \cos (2x-1) \; dx=\cos (2x-1)\cdot \left(\frac{3x^2}{2}+4x \right) - \int \left(\frac{3x^2}{2}+4x \right) \cdot (-2\sin(2x-1)dx)=\\ =\cos (2x-1)\cdot \left(\frac{3x^2}{2}+4x \right) +2\cdot\int \left(\frac{3x^2}{2}+4x \right) \sin(2x-1)\;dx $$
И к чему мы пришли? Мы пришли к интегралу $\int \left(\frac{3x^2}{2}+4x \right) \sin(2x-1)\;dx$, который явно сложнее нежели исходный интеграл $\int (3x+4) \cos (2x-1) \; dx$. Это говорит о том, что выбор $u$ и $dv$ был сделан неудачно. После применения формулы интегрирования по частям полученный интеграл должен быть проще исходного. Находя неопределенный интеграл по частям мы должны упрощать его, а не усложнять, поэтому если после применения формулы (1) интеграл усложнился, то выбор $u$ и $dv$ осуществлён некорректно.
Пример №2
Найти $\int (3x^4+4x-1) \ln 5x \; dx$.
Под интегралом расположен многочлен (т.е. $3x^4+4x-1$) и $\ln 5x$. Этот случай подпадает под , поэтому возьмём интеграл по частям. Заданный интеграл имеет такую же структуру, как и интеграл $\int P_n(x) \ln x\; dx$. Вновь, как и в примере №1, нам нужно выбрать какую-то часть подынтегрального выражения $(3x^4+4x-1) \ln 5x \; dx$ в качестве $u$, а какую-то часть - в качестве $dv$. Согласно , нужно выбрать $dv=P_n(x)dx$, т.е. в нашем случае $dv=(3x^4+4x-1)dx$. Если из выражения $(3x^4+4x-1) \ln 5x \; dx$ "изьять" $dv=(3x^4+4x-1)dx$, то останется $\ln 5x$ - это и будет функция $u$. Итак, $dv=(3x^4+4x-1)dx$, $u=\ln 5x$. Для применения формулы нам понадобятся также $du$ и $v$. Так как $u=\ln 5x$, то:
$$ du=d(\ln 5x)=(\ln 5x)"dx=\frac{1}{5x}\cdot 5 dx=\frac{1}{x}dx. $$
Теперь найдём функцию $v$. Так как $dv=(3x^4+4x-1)dx$, то:
$$ v=\int(3x^4+4x-1)\; dx=\frac{3x^5}{5}+2x^2-x+C. $$
Из всего найденного бесконечного множества функций $\frac{3x^5}{5}+2x^2-x+C$ нам нужно выбрать одну. А проще всего это сделать приняв $C=0$, т.е. $v=\frac{3x^5}{5}+2x^2-x$. Для применения формулы всё готово. Подставим в правую часть указанной формулы значения $u=\ln 5x$, $du=\frac{1}{x}dx$, $v=\frac{3x^5}{5}+2x^2-x$ и $dv=(3x^4+4x-1)dx$ будем иметь:
$$ \int (3x^4+4x-1) \ln 5x \; dx=\left | \begin{aligned} & u=\ln 5x; \; du=\frac{1}{x}dx.\\ & dv=(3x^4+4x-1)dx; \; v=\frac{3x^5}{5}+2x^2-x. \end{aligned} \right |=\\ =\ln 5x \cdot \left (\frac{3x^5}{5}+2x^2-x \right)-\int \left (\frac{3x^5}{5}+2x^2-x \right)\cdot \frac{1}{x}dx=\\ =\left (\frac{3x^5}{5}+2x^2-x \right)\cdot\ln 5x -\int \left (\frac{3x^4}{5}+2x-1 \right)dx=\\ =\left (\frac{3x^5}{5}+2x^2-x \right)\cdot\ln 5x - \left (\frac{3x^5}{25}+x^2-x \right)+C=\\ =\left (\frac{3x^5}{5}+2x^2-x \right)\cdot\ln 5x - \frac{3x^5}{25}-x^2+x+C. $$
Ответ : $\int (3x^4+4x-1) \ln 5x \; dx=\left (\frac{3x^5}{5}+2x^2-x \right)\cdot\ln 5x - \frac{3x^5}{25}-x^2+x+C$.
Пример №3
Найти $\int \arccos x \; dx$.
Этот интеграл имеет структуру $\int P_n(x) \arccos x \;dx$, подпадающую под . Понимаю, что сразу возникнет резонный вопрос: "а где в заданном интеграле $\int\arccos x \; dx$ спрятали многочлен $P_n(x)$? Там же нет никакого многочлена, только арккосинус и всё!". Однако на самом деле под интегралом расположен не только арккосинус. Я представлю интеграл $\int arccos x \; dx$ в таком виде: $\int 1\cdot\arccos x \; dx$. Согласитесь, что от домножения на единицу подынтегральное выражение не изменится. Вот эта единица и есть $P_n(x)$. Т.е. $dv=1\cdot dx=dx$. А в качестве $u$ (согласно ) принимаем $\arccos x$, т.е. $u=\arccos x$. Значения $du$ и $v$, кои учавствуют в формуле , найдём так же, как и в предыдущих примерах:
$$ du=(\arccos x)"dx=-\frac{1}{\sqrt{1-x^2}}dx;\\ v=\int 1\; dx=x+C. $$
Как и в предыдущих примерах, полагая $C=0$ получим $v=x$. Подставляя все найденные параметры в формулу , будем иметь следующее:
$$ \int \arccos x \; dx=\left | \begin{aligned} & u=\arccos x; \; du=-\frac{1}{\sqrt{1-x^2}}dx.\\ & dv=dx; \; v=x. \end{aligned} \right |=\\ =\arccos x \cdot x-\int x\cdot \left(-\frac{1}{\sqrt{1-x^2}}dx \right)= \arccos x \cdot x+\int \frac{xdx}{\sqrt{1-x^2}}=\\ =x\cdot\arccos x-\frac{1}{2}\cdot\int (1-x^2)^{-\frac{1}{2}}d(1-x^2)= =x\cdot\arccos x-\frac{1}{2}\cdot\frac{(1-x^2)^{\frac{1}{2}}}{\frac{1}{2}}+C=\\ =x\cdot\arccos x-\sqrt{1-x^2}+C. $$
Ответ : $\int\arccos x \; dx=x\cdot\arccos x-\sqrt{1-x^2}+C$.
Пример №4
Найти $\int (3x^2+x) e^{7x} \; dx$.
В этом примере формулу интегрирования по частям придётся применять два раза. Интеграл $\int (3x^2+x) e^{7x} \; dx$ имеет структуру $\int P_n(x) a^x \;dx$. В нашем случае $P_n(x)=3x^2+x$, $a=e$. Согласно имеем: $u=3x^2+x$. Соответственно, $dv=e^{7x}dx$.
$$ du=(3x^2+x)"=(6x+1)dx;\\ v=\int e^{7x}\;dx=\frac{1}{7}\cdot \int e^{7x}\;d(7x)=\frac{1}{7}\cdot e^{7x}+C=\frac{e^{7x}}{7}+C. $$
Опять-таки, как и в предыдущих примерах, полагая $C=0$, имеем: $v=\frac{e^{7x}}{7}$.
$$ \int (3x^2+x) e^{7x} \; dx=\left | \begin{aligned} & u=3x^2+x; \; du=(6x+1)dx.\\ & dv=e^{7x}dx; \; v=\frac{e^{7x}}{7}. \end{aligned} \right |=\\ =(3x^2+x)\cdot\frac{e^{7x}}{7}-\int \frac{e^{7x}}{7}\cdot (6x+1)dx= \frac{(3x^2+x)e^{7x}}{7}-\frac{1}{7}\cdot \int (6x+1) e^{7x}\;dx. $$
Мы пришли к интегралу $\int (6x+1) e^{7x}\;dx$, который вновь необходимо брать по частям. Приняв $u=6x+1$ и $dv=e^{7x}dx$ будем иметь:
$$ \frac{(3x^2+x)e^{7x}}{7}-\frac{1}{7}\cdot \int (6x+1) e^{7x}\;dx=\left | \begin{aligned} & u=6x+1; \; du=6dx.\\ & dv=e^{7x}dx; \; v=\frac{e^{7x}}{7}. \end{aligned} \right |=\\ =\frac{(3x^2+x)e^{7x}}{7}-\frac{1}{7}\cdot \left ((6x+1)\cdot\frac{e^{7x}}{7} - \int\frac{e^{7x}}{7}\cdot 6\;dx \right)=\\ =\frac{(3x^2+x)e^{7x}}{7} -\frac{(6x+1)e^{7x}}{49} +\frac{6}{49}\cdot\int\ e^{7x}\;dx=\\ =\frac{(3x^2+x)e^{7x}}{7} -\frac{(6x+1)e^{7x}}{49} +\frac{6}{49}\cdot\frac{e^{7x}}{7}+C=\\ =\frac{(3x^2+x)e^{7x}}{7} -\frac{(6x+1)e^{7x}}{49} +\frac{6\; e^{7x}}{343}+C. $$
Полученный ответ можно и упростить, раскрыв скобки и перегруппировав слагаемые:
$$ \frac{(3x^2+x)e^{7x}}{7} -\frac{(6x+1)e^{7x}}{49} +\frac{6\; e^{7x}}{343}+C=e^{7x}\cdot \left(\frac{3x^2}{7}+\frac{x}{49}-\frac{1}{343} \right)+C. $$
Ответ : $\int (3x^2+x) e^{7x} \; dx=e^{7x}\cdot \left(\frac{3x^2}{7}+\frac{x}{49}-\frac{1}{343} \right)+C$.
Пример №5
Найти $\int (x^2+5)\sin(3x+1) \; dx$.
Здесь, как и в предыдущем примере, интегрирование по частям применяется дважды. Подробные пояснения были даны ранее, поэтому приведу только решение:
$$ \int (x^2+5)\sin(3x+1) \; dx=\left | \begin{aligned} & u=x^2+5; \; du=2xdx.\\ & dv=\sin(3x+1)dx; \; v=-\frac{\cos(3x+1)}{3}. \end{aligned} \right |=\\ =(x^2+5)\cdot \left(-\frac{\cos(3x+1)}{3} \right)-\int\left(-\frac{\cos(3x+1)}{3} \right)\cdot 2xdx=\\ = -\frac{(x^2+5)\cdot\cos(3x+1)}{3} +\frac{2}{3}\int x\cos(3x+1)dx= \left | \begin{aligned} & u=x; \; du=dx.\\ & dv=\cos(3x+1)dx; \; v=\frac{\sin(3x+1)}{3}. \end{aligned} \right |=\\ =-\frac{(x^2+5)\cdot\cos(3x+1)}{3} +\frac{2}{3}\cdot \left(x\cdot\frac{\sin(3x+1)}{3}-\int\frac{\sin(3x+1)}{3}dx \right)=\\ =-\frac{(x^2+5)\cdot\cos(3x+1)}{3} +\frac{2x\sin(3x+1)}{9}-\frac{2}{9}\cdot\int\sin(3x+1)dx=\\ =-\frac{(x^2+5)\cdot\cos(3x+1)}{3} +\frac{2x\sin(3x+1)}{9}-\frac{2}{9}\cdot \left(-\frac{\cos(3x+1)}{3}\right)+C=\\ = -\frac{(x^2+5)\cdot\cos(3x+1)}{3} +\frac{2x\sin(3x+1)}{9}+\frac{2\cos(3x+1)}{27}+C=\\ =-\frac{x^2\cdot\cos(3x+1)}{3}-\frac{5\cdot\cos(3x+1)}{3} +\frac{2x\sin(3x+1)}{9}+\frac{2\cos(3x+1)}{27}+C=\\ =-\frac{x^2\cdot\cos(3x+1)}{3} +\frac{2x\sin(3x+1)}{9}-\frac{43\cos(3x+1)}{27}+C. $$
Ответ : $\int (x^2+5)\sin(3x+1) \; dx=-\frac{x^2\cdot\cos(3x+1)}{3} +\frac{2x\sin(3x+1)}{9}-\frac{43\cos(3x+1)}{27}+C$.
Применение метода интегрирования по частям в несколько нестандартных случаях, не подпадающих под действие правил №1 и №2, будет дано во
Следующая формула называется формулой интегрирования по частям в неопределённом интеграле:
Для применения формулы интегрирования по частям подынтегральное выражение нужно разбить на два множителя. Один из них обозначается через u , а остальная часть относится ко второму множителю и обозначается через dv . Затем дифференцированием находится du и интегрированием - функция v . При этом за u dv - такую часть подынтегрального выражения, которая легко интегрируется.
Когда выгодно применять метод интегрирования по частям? Тогда, когда подынтегральная функция содержит :
1) - логарифмические функции, а также обратные тригонометрические функции (с приставкой "arc"), тогда на основании продолжительного опыта интегрирования по частям эти функции обозначаются через u ;
2) , , - синус, косинус и экспоненту, умноженные на P (x ) - произвольный многочлен от икса, тогда эти функции обозначают через dv , а многочлен - через u ;
3) , , , , в этом случае интегрирование по частям применяется дважды.
Поясним ценность метода интегрирования по частям на примере первого случая. Пусть выражение под знаком интеграла содержит логарифмическую функцию (таким будет пример 1). Применением интегрирования по частям такой интеграл сводится вычислению интеграла только алгебраических функций (чаще всего многочлена), то есть не содержащих логарифмическую или обратную тригонометрическую функцию. Применяя данную в самом начале урока формулу интегрирования по частям
получаем в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) - функцию, не содержащую логарифма. Интеграл алгебраической функции намного проще интеграла, под знаком которого находятся отдельно или вместе с алгебраическим множителем логарифмическая или обратная тригонометрическая функция.
Таким образом, с помощью формулы интегрирования по частям интегрирование не выполняется сразу: нахождение данного интеграла сводится к нахождению другого. Смысл формулы интегрирования по частям состоит в том, чтобы в результате её применения новый интеграл оказался табличным или хотя бы стал проще первоначального.
Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций:
то её можно записать в виде
который и был приведён в самом начале урока.
При нахождении интегрированием функции v для неё получается бесконечное множество первообразных функций. Чтобы применить формулу интегрирования по частям, можно взять любую из них, а значит, и ту, которая соответствует произвольной постоянной С , равной нулю. Поэтому при нахождении функции v произвольную постоянную С вводить не следует.
Есть у метода интегрирования по частям совершенно особенное применение: с его помощью можно выводить рекуррентные формулы для нахождения первообразных функций, когда требуется понизить степень функций под знаком интеграла. Понижение степени необходимо, когда не существует табличных интегралов для таких, например, функций, как синусы и косинусы в степени более второй и их произведения. Рекуррентная формула - это формула для нахождения очередного члена последовательности через предыдущий член. Для обозначенных случаев цель достигается последовательным понижением степени. Так, если подынтегральная функция - синус в четвёртой степени от икса, то методом интегрирования по частям можно найти формулу для интеграла синуса в третьей степени и так далее. Описанной задаче посвящен последний параграф этого урока.
Применяем интегрирование по частям вместе
Пример 1. Найти неопределённый интеграл методом интегрирования по частям :
Решение. В подынтегральном выражении - логарифм, который, как мы уже знаем, разумно обозначить через u . Полагаем, что , .
Находим (как уже говорилось в пояснении к теоретической справке, сразу же получаем в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) - функцию, не содержащую логарифма):
И снова логарифм...
Пример 2. Найти неопределённый интеграл:
Решение. Пусть , .
Логарифм присутствует в квадрате. Это значит, что его нужно дифференцировать как сложную функцию. Находим
,
.
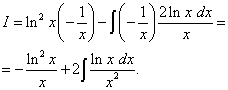
Второй интеграл вновь находим по частям и получаем уже упомянутое преимущество (в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) - функцию, не содержащую логарифма).
Находим изначальный интеграл:
Пример 3.
Решение. Арктангенс, как и логарифм, лучше обозначить через u . Итак, пусть , .
Тогда
,
.
Применяя формулу интегрирования по частям, получаем:
Второй интеграл находим методом замены переменной.
Возвращаясь к переменной x , получаем
.
Находим изначальный интеграл:
.
Пример 4. Найти неопределённый интеграл методом интегрирования по частям :
Решение. Экспоненту лучше обозначить через dv
. Разбиваем подынтегральное выражение на два множителя. Полагая, что
Пример 5. Найти неопределённый интеграл методом интегрирования по частям :
.
Решение. Пусть , . Тогда , .
Используя формулу интегрирования по частям (1), находим:
Пример 6. Найти неопределённый интеграл методом интегрирования по частям:
Решение. Синус, как и экспоненту, удобно обозначить через dv . Пусть , .
По формуле интегрирования по частям находим:
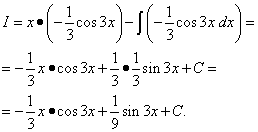
Снова применяем интегрирование по частям вместе
Пример 10. Найти неопределённый интеграл методом интегрирования по частям:
.
Решение. Как и во всех подобных случаях, косинус удобно обозначить через dv . Обозначаем , .
Тогда 
,
.
По формуле интегрирования по частям получаем:
Ко второму слагаемому также применяем интегрирование по частям. Обозначаем , .
Применив эти обозначения, интегрируем упомянутое слагаемое:
Теперь находим требуемый интеграл:
Среди интегралов, которые можно решить методом интегрирования по частям, есть и такие, которые не входят ни в одну из трёх упомянутых в теоретической части групп, относительно которых из практики известно, что лучше обозначать через u , а что через dv . Поэтому в этих случаях нужно пользоваться соображением удобства, также приведённым в параграфе "Суть метода интегрирования по частям": за u следует брать такую часть подынтегральной функции, которая при дифференцировании сильно не усложняется, а за dv - такую часть подынтегрального выражения, которая легко интегрируется. Последний пример этого урока - решение именно такого интеграла.
