Собственные векторы и собственные значения матрицы онлайн с решением. Собственные числа и собственные векторы матрицы

www.сайт позволяет найти . Сайт производит вычисление . За неколько секунд сервер выдаст правильное решение. Характеристическим уравнение для матрицы будет являться алгебраическое выражение, найденное по правилу вычисления определителя матрицы матрицы , при этом по главной диагонали будут стоять разницы значений диагональных элементов и переменной. При вычислении характеристического уравнения для матрицы онлайн , каждый элемент матрицы будет перемножаться с соответствующими другими элементами матрицы . Найти в режиме онлайн можно только для квадратной матрицы . Операция нахождения характеристического уравнения для матрицы онлайн сводится к вычислению алгебраической суммы произведения элементов матрицы как результат от нахождения определителя матрицы , только с целью определения характеристического уравнения для матрицы онлайн . Данная операция занимает особое место в теории матриц , позволяет найти собственные числа и векторы, используя корни . Задача по нахождению характеристического уравнения для матрицы онлайн заключается в перемножении элементов матрицы с последующим суммированием этих произведений по определенному правилу. www.сайт находит характеристическое уравнение для матрицы заданной размерности в режиме онлайн . Вычисление характеристического уравнения для матрицы онлайн при заданной её размерности - это нахождение многочлена с числовыми или символьными коэффициентами, найденного по правилу вычисления определителя матрицы - как сумма произведений соответствующих элементов матрицы , только с целью определения характеристического уравнения для матрицы онлайн . Нахождение полинома относительно переменной для квадратной матрицы , как определение характеристического уравнения для матрицы , распространено в теории матриц . Значение корней многочлена характеристического уравнения для матрицы онлайн используется для определения собственных векторов и собственных чисел для матрицы . При этом, если определитель матрицы будет равен нулю, то характеристическое уравнение матрицы все равно будет существовать, в отличии от обратной матрицы . Для того, чтобы вычислить характеристическое уравнение для матрицы или найти сразу для нескольких матриц характеристические уравнения , необходимо затратить не мало времени и усилий, в то время как наш сервер в считанные секунды найдет характеристическое уравнение для матрицы онлайн . При этом ответ по нахождению характеристического уравнения для матрицы онлайн будет правильным и с достаточной точностью, даже если числа при нахождении характеристического уравнения для матрицы онлайн будут иррациональными. На сайте www.сайт допускаются символьные записи в элементах матриц , то есть характеристическое уравнение для матрицы онлайн может быть представлено в общем символьном виде при вычислении характеристического уравнения матрицы онлайн . Полезно проверить ответ, полученный при решении задачи по нахождению характеристического уравнения для матрицы онлайн , используя сайт www.сайт . При совершении операции вычисления полинома - характеристического уравнения матрицы , необходимо быть внимательным и предельно сосредоточенным при решении данной задачи. В свою очередь наш сайт поможет Вам проверить своё решение на тему характеристическое уравнение матрицы онлайн . Если у Вас нет времени на долгие проверки решенных задач, то www.сайт безусловно будет являться удобным инструментом для проверки при нахождении и вычислении характеристического уравнения для матрицы онлайн .

Собственный вектор квадратной матрицы - это такой вектор, который при умножении на заданную матрицу дает в результате коллинеарный вектор. Простыми словами, при умножении матрицы на собственный вектор последний остается тем же самым, но умноженным на некоторое число.

Определение

Собственный вектор - это ненулевой вектор V, который при умножении на квадратную матрицу Mпревращается в самого себя, увеличенного на некоторое число λ. В алгебраической записи это выглядит как:

M × V = λ × V,

где λ - собственное число матрицы M.

Рассмотрим числовой пример. Для удобства записи числа в матрице будет отделять точкой с запятой. Пусть у нас есть матрица:

• M = 0; 4;
• 6; 10.

Умножим ее на вектор-столбец:

• V = -2;

При умножении матрицы на вектор-столбец мы получаем также вектор-столбец. Строгим математическим языком формула умножения матрицы 2 × 2 на вектор-столбец будет выглядеть так:

• M × V = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21.

М11 означает элемент матрицы M, стоящий в первой строке и первом столбце, а M22 - элемент, расположенные во второй строке и втором столбце. Для нашей матрицы эти элементы равны M11 = 0, М12 = 4, М21 = 6, М22 10. Для вектора-столбца эти значения равны V11 = –2, V21 = 1. Согласно этой формуле мы получим следующий результат произведения квадратной матрицы на вектор:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Для удобства запишем вектор столбец в строку. Итак, мы умножили квадратную матрицу на вектор (-2; 1), в результате чего получили вектор (4; -2). Очевидно, что это тот же вектор, умноженный на λ = -2. Лямбда в данном случае обозначает собственное число матрицы.

Собственный вектор матрицы - это коллинеарный вектор, то есть объект, который не изменяет своего положения в пространстве при умножении его на матрицу. Понятие коллинеарности в векторной алгебре сходно с термином параллельности в геометрии. В геометрической интерпретации коллинеарные вектора - это параллельные направленные отрезки разной длины. Еще со времен Евклида мы знаем, что у одной прямой существует бесконечное количество параллельных ей прямых, поэтому логично предположить, что каждая матрица обладает бесконечным количеством собственных векторов.

Из предыдущего примера видно, что собственными векторами могут быть и (-8; 4), и (16; -8), и (32, -16). Все это коллинеарные вектора, соответствующие собственному числу λ = -2. При умножении исходной матрицы на эти вектора мы все так же будет получать в результате вектор, который отличается от исходного в 2 раза. Именно поэтому при решении задач на поиск собственного вектора требуется найти только линейно независимые векторные объекты. Чаще всего для матрицы размером n × n существует n-ное количество собственных векторов. Наш калькулятор заточен под анализ квадратных матриц второго порядка, поэтому практически всегда в результате будут найдены два собственных вектора, за исключением случаев, когда они совпадают.

В примере выше мы заранее знали собственный вектор исходной матрицы и наглядно определили число лямбда. Однако на практике все происходит наоборот: в начале находится собственные числа и только затем собственные вектора.

Алгоритм решения

Давайте вновь рассмотрим исходную матрицу M и попробуем найти оба ее собственных вектора. Итак, матрица выглядит как:

• M = 0; 4;
• 6; 10.

Для начала нам необходимо определить собственное число λ, для чего требуется вычислить детерминант следующей матрицы:

• (0 − λ); 4;
• 6; (10 − λ).

Данная матрица получена путем вычитания неизвестной λ из элементов на главной диагонали. Детерминант определяется по стандартной формуле:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Так как наш вектор должен быть не нулевым, полученное уравнение принимаем как линейно зависимое и приравниваем наш детерминант detA к нулю.

(0 − λ) × (10 − λ) − 24 = 0

Раскроем скобки и получим характеристическое уравнение матрицы:

λ 2 − 10λ ­− 24 = 0

Это стандартное квадратное уравнение, которое требуется решить через дискриминант.

D = b 2 − 4ac = (-10) × 2 − 4 × (-1) × 24 = 100 + 96 = 196

Корень из дискриминанта равен sqrt(D) = 14, следовательно, λ1 = -2, λ2 = 12. Теперь для каждого значения лямбда требуется найти собственный вектор. Выразим коэффициенты системы для λ = -2.

• М − λ × E = 2; 4;
• 6; 12.

В данной формуле E - это единичная матрица. На основании полученной матрицы составим систему линейных уравнений:

2x + 4y = 6x + 12y,

где x и y - элементы собственного вектора.

Соберем все иксы слева, а все игреки справа. Очевидно, что - 4x = 8y. Разделим выражение на - 4 и получим x = –2y. Теперь мы можем определить первый собственный вектор матрицы, приняв любые значения неизвестных (вспоминаем про бесконечность линейно зависимых собственных векторов). Примем y = 1, тогда x = –2. Следовательно, первый собственный вектор выглядит как V1 = (–2; 1). Вернитесь в начало статьи. Именно на этот векторный объект мы умножали матрицу для демонстрации понятия собственного вектора.

Теперь отыщем собственный вектор для λ = 12.

• М - λ × E = -12; 4
• 6; -2.

Составим такую же систему линейных уравнений;

• -12x + 4y = 6x − 2y
• -18x = -6y
• 3x = y.

Теперь примем x = 1, следовательно, y = 3. Таким образом, второй собственный вектор выглядит как V2 = (1; 3). При умножении исходной матрицы на данный вектор, в результате всегда будет такой же вектор, умноженный на 12. На этом алгоритм решения заканчивается. Теперь вы знаете, как вручную определить собственный вектор матрицы.

• определитель;
• след, то есть сумму элементов на главной диагонали;
• ранг, то есть максимальное количество линейно независимых строк/столбцов.

Программа действует по выше приведенному алгоритму, максимально сокращая процесс решения. Важно указать, что в программе лямбда обозначена литерой «c». Давайте рассмотрим численный пример.

Пример работы программы

Попробуем определить собственные вектора для следующей матрицы:

• M = 5; 13;
• 4; 14.

Введем эти значения в ячейки калькулятора и получим ответ в следующем виде:

• Ранг матрицы: 2;
• Детерминант матрицы: 18;
• След матрицы: 19;
• Расчет собственного вектора: c 2 − 19,00c + 18,00 (характеристическое уравнение);
• Расчет собственного вектора: 18 (первое значение лямбда);
• Расчет собственного вектора: 1 (второе значение лямбда);
• Система уравнений вектора 1: -13x1 + 13y1 = 4x1 − 4y1;
• Система уравнений вектора 2: 4x1 + 13y1 = 4x1 + 13y1;
• Собственный вектор 1: (1; 1);
• Собственный вектор 2: (-3,25; 1).

Таким образом, мы получили два линейно независимых собственных вектора.

Заключение

Линейная алгебра и аналитическая геометрия - стандартные предметы для любого первокурсника технической специальности. Большое количество векторов и матриц приводит в ужас, а в столь громоздких вычислениях легко сделать ошибку. Наша программа позволит студентам проверить свои выкладки или автоматически решит задачу на поиск собственного вектора. В нашем каталоге есть и другие калькуляторы по линейной алгебре, используйте их в своей учебе или работе.

Наиболее просто устроены матрицы диагонального вида . Возникает вопрос, нельзя ли найти базис, в котором матрица линейного оператора имела бы диагональный вид. Такой базис существует.
Пусть дано линейное пространство R n и действующий в нем линейный оператор A; в этом случае оператор A переводит R n в себя, то есть A:R n → R n .

Определение. Ненулевой вектор называется собственным вектором оператора A , если оператор A переводит в коллинеарный ему вектор, то есть . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов оператора A, отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы оператора A с попарно различными собственными числами λ 1 , λ 2 , …, λ m линейно независимы.
3. Если собственные числа λ 1 =λ 2 = λ m = λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.

Итак, если имеется n линейно независимых собственных векторов , соответствующих различным собственным числам λ 1 , λ 2 , …, λ n , то они линейно независимы, следовательно, их можно принять за базис пространства R n . Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: тогда .
Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.

Теорема. Матрица линейного оператора A в базисе (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса - собственные векторы оператора A.

Правило отыскания собственных чисел и собственных векторов

. (*)

(1)
где - матрица линейного оператора.

Система (1) имеет ненулевое решение, если ее определитель D равен нулю

Пример 12. Линейный оператор A действует в R 3 по закону , где x 1 , x 2 , .., x n - координаты вектора в базисе , , . Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
.
Составляем систему для определения координат собственных векторов:

Составляем характеристическое уравнение и решаем его:

.
λ 1,2 = -1, λ 3 = 3.
Подставляя λ = -1 в систему, имеем:
или
Так как , то зависимых переменных два, а свободное одно.
Пусть x 1 - свободное неизвестное, тогда Решаем эту систему любым способом и находим общее решение этой системы: Фундаментальная система решений состоит из одного решения, так как n - r = 3 - 2 = 1.
Множество собственных векторов, отвечающих собственному числу λ = -1, имеет вид: , где x 1 - любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив x 1 = 1: .
Рассуждая аналогично, находим собственный вектор, отвечающий собственному числу λ = 3: .
В пространстве R 3 базис состоит из трех линейно независимых векторов, мы же получили только два линейно независимых собственных вектора, из которых базис в R 3 составить нельзя. Следовательно, матрицу A линейного оператора привести к диагональному виду не можем.

Пример 13. Дана матрица .
1. Доказать, что вектор является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.
Решение.
1. Если , то - собственный вектор

.
Вектор (1, 8, -1) - собственный вектор. Собственное число λ = -1.
Диагональный вид матрица имеет в базисе, состоящем из собственных векторов. Один из них известен. Найдем остальные.
Собственные векторы ищем из системы:

Характеристическое уравнение: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Найдем собственный вектор, отвечающий собственному числу λ = -3:

Ранг матрицы этой системы равен двум и равен числу неизвестных, поэтому эта система имеет только нулевое решение x 1 = x 3 = 0. x 2 здесь может быть любым, отличным от нуля, например, x 2 = 1. Таким образом, вектор (0,1,0) является собственным вектором, отвечающим λ = -3. Проверим:
.
Если λ = 1, то получаем систему
Ранг матрицы равен двум. Последнее уравнение вычеркиваем.
Пусть x 3 - свободное неизвестное. Тогда x 1 = -3x 3 , 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3 , x 2 = -9x 3 .
Полагая x 3 = 1, имеем (-3,-9,1) - собственный вектор, отвечающий собственному числу λ = 1. Проверка:

.
Так как собственные числа действительные и различны, то векторы, им отвечающие, линейно независимы, поэтому их можно принять за базис в R 3 . Таким образом, в базисе , , матрица A имеет вид:
.
Не всякую матрицу линейного оператора A:R n → R n можно привести к диагональному виду, поскольку для некоторых линейных операторов линейно независимых собственных векторов может быть меньше n. Однако, если матрица симметрическая, то корню характеристического уравнения кратности m соответствует ровно m линейно независимых векторов.

Определение. Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой .
Замечания. 1. Все собственные числа симметрической матрицы вещественны.
2. Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.
В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.

С матрицей А, если найдется такое число l, что АХ = lХ.

При этом число l называют собственным значением оператора (матрицы А), соответствующим вектору Х.

Иными словами, собственный вектор - это такой вектор, который под действием линейного оператора переходит в коллинеарный вектор, т.е. просто умножается на некоторое число. В отличие от него, несобственные векторы преобразуются более сложно.

Запишем определение собственного вектора в виде системы уравнений:

Перенесем все слагаемые в левую часть:

Последнюю систему можно записать в матричной форме следующим образом:

(А - lЕ)Х = О

Полученная система всегда имеет нулевое решение Х = О. Такие системы, в которых все свободные члены равны нулю, называют однородными . Если матрица такой системы - квадратная, и ее определитель не равен нулю, то по формулам Крамера мы всегда получим единственное решение - нулевое. Можно доказать, что система имеет ненулевые решения тогда и только тогда, когда определитель этой матрицы равен нулю, т.е.

|А - lЕ| = = 0

Это уравнение с неизвестным l называют характеристическим уравнением (характеристическим многочленом ) матрицы А (линейного оператора).

Можно доказать, что характеристический многочлен линейного оператора не зависит от выбора базиса.

Например, найдем собственные значения и собственные векторы линейного оператора, заданного матрицей А = .

Для этого составим характеристическое уравнение |А - lЕ| = = (1 - l) 2 - 36 = 1 - 2l + l 2 - 36 = l 2 - 2l - 35 = 0; Д = 4 + 140 = 144; собственные значения l 1 = (2 - 12)/2 = -5; l 2 = (2 + 12)/2 = 7.

Чтобы найти собственные векторы, решаем две системы уравнений

(А + 5Е)Х = О

(А - 7Е)Х = О

Для первой из них расширенная матрица примет вид

,

откуда х 2 = с, х 1 + (2/3)с = 0; х 1 = -(2/3)с, т.е. Х (1) = (-(2/3)с; с).

Для второй из них расширенная матрица примет вид

,

откуда х 2 = с 1 , х 1 - (2/3)с 1 = 0; х 1 = (2/3)с 1 , т.е. Х (2) = ((2/3)с 1 ; с 1).

Таким образом, собственными векторами этого линейного оператора являются все вектора вида (-(2/3)с; с) с собственным значением (-5) и все вектора вида ((2/3)с 1 ; с 1) с собственным значением 7.

Можно доказать, что матрица оператора А в базисе, состоящем из его собственных векторов, является диагональной и имеет вид:

,

где l i - собственные значения этой матрицы.

Верно и обратное: если матрица А в некотором базисе является диагональной, то все векторы этого базиса будут собственными векторами этой матрицы.

Также можно доказать, что если линейный оператор имеет n попарно различных собственных значений, то соответствующие им собственные векторы линейно независимы, а матрица этого оператора в соответствующем базисе имеет диагональный вид.

Поясним это на предыдущем примере. Возьмем произвольные ненулевые значения с и с 1 , но такие, чтобы векторы Х (1) и Х (2) были линейно независимыми, т.е. образовали бы базис. Например, пусть с = с 1 = 3, тогда Х (1) = (-2; 3), Х (2) = (2; 3).

Убедимся в линейной независимости этих векторов:

12 ≠ 0. В этом новом базисе матрица А примет вид А * = .

Чтобы убедиться в этом, воспользуемся формулой А * = С -1 АС. Вначале найдем С -1 .

С -1 = ;

Квадратичные формы

Квадратичной формой f(х 1 , х 2 , х n) от n переменных называют сумму, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятым с некоторым коэффициентом: f(х 1 , х 2 , х n) = (a ij = a ji).

Матрицу А, составленную из этих коэффициентов, называют матрицей квадратичной формы . Это всегда симметрическая матрица (т.е. матрица, симметричная относительно главной диагонали, a ij = a ji).

В матричной записи квадратичная форма имеет вид f(Х) = Х Т AX, где

В самом деле

Например, запишем в матричном виде квадратичную форму .

Для этого найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, а остальные элементы - половинам соответствующих коэффициентов квадратичной формы. Поэтому

Пусть матрица-столбец переменных X получена невырожденным линейным преобразованием матрицы-столбца Y, т.е. X = CY, где С - невырожденная матрица n-го порядка. Тогда квадратичная форма f(X) = Х T АХ = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

Таким образом, при невырожденном линейном преобразовании С матрица квадратичной формы принимает вид: А * = C T AC.

Например, найдем квадратичную форму f(y 1 , y 2), полученную из квадратичной формы f(х 1 , х 2) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 линейным преобразованием .

Квадратичная форма называется канонической (имеет канонический вид ), если все ее коэффициенты a ij = 0 при i ≠ j, т.е.
f(х 1 , х 2 , х n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 = .

Ее матрица является диагональной.

Теорема (доказательство здесь не приводится). Любая квадратичная форма может быть приведена к каноническому виду с помощью невырожденного линейного преобразования.

Например, приведем к каноническому виду квадратичную форму
f(х 1 , х 2 , х 3) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 - х 2 х 3 .

Для этого вначале выделим полный квадрат при переменной х 1:

f(х 1 , х 2 , х 3) = 2(x 1 2 + 2х 1 х 2 + х 2 2) - 2х 2 2 - 3х 2 2 - х 2 х 3 = 2(x 1 + х 2) 2 - 5х 2 2 - х 2 х 3 .

Теперь выделяем полный квадрат при переменной х 2:

f(х 1 , х 2 , х 3) = 2(x 1 + х 2) 2 - 5(х 2 2 + 2* х 2 *(1/10)х 3 + (1/100)х 3 2) + (5/100)х 3 2 =
= 2(x 1 + х 2) 2 - 5(х 2 - (1/10)х 3) 2 + (1/20)х 3 2 .

Тогда невырожденное линейное преобразование y 1 = x 1 + х 2 , y 2 = х 2 + (1/10)х 3 и y 3 = x 3 приводит данную квадратичную форму к каноническому виду f(y 1 , y 2 , y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .

Отметим, что канонический вид квадратичной формы определяется неоднозначно (одна и та же квадратичная форма может быть приведена к каноническому виду разными способами). Однако полученные различными способами канонические формы обладают рядом общих свойств. В частности, число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду (например, в рассмотренном примере всегда будет два отрицательных и один положительный коэффициент). Это свойство называют законом инерции квадратичных форм.

Убедимся в этом, по-другому приведя ту же квадратичную форму к каноническому виду. Начнем преобразование с переменной х 2:

f(х 1 , х 2 , х 3) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 - х 2 х 3 = -3х 2 2 - х 2 х 3 + 4х 1 х 2 + 2x 1 2 = -3(х 2 2 +
+ 2* х 2 ((1/6) х 3 - (2/3)х 1) + ((1/6) х 3 - (2/3)х 1) 2) + 3((1/6) х 3 - (2/3)х 1) 2 + 2x 1 2 =
= -3(х 2 + (1/6) х 3 - (2/3)х 1) 2 + 3((1/6) х 3 + (2/3)х 1) 2 + 2x 1 2 = f(y 1 , y 2 , y 3) = -3y 1 2 -
+3y 2 2 + 2y 3 2 , где y 1 = - (2/3)х 1 + х 2 + (1/6) х 3 , y 2 = (2/3)х 1 + (1/6) х 3 и y 3 = x 1 . Здесь отрицательный коэффициент -3 при y 1 и два положительных коэффициента 3 и 2 при y 2 и y 3 (а при использовании другого способа мы получили отрицательный коэффициент (-5) при y 2 и два положительных: 2 при y 1 и 1/20 при y 3).

Также следует отметить, что ранг матрицы квадратичной формы, называемый рангом квадратичной формы , равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.

Квадратичную форму f(X) называют положительно (отрицательно ) определенной , если при всех значениях переменных, не равных одновременно нулю, она положительна, т.е. f(X) > 0 (отрицательна, т.е.
f(X) < 0).

Например, квадратичная форма f 1 (X) = x 1 2 + х 2 2 - положительно определенная, т.к. представляет собой сумму квадратов, а квадратичная форма f 2 (X) = -x 1 2 + 2x 1 х 2 - х 2 2 - отрицательно определенная, т.к. представляет ее можно представить в виде f 2 (X) = -(x 1 - х 2) 2 .

В большинстве практических ситуации установить знакоопределенность квадратичной формы несколько сложнее, поэтому для этого используют одну из следующих теорем (сформулируем их без доказательств).

Теорема . Квадратичная форма является положительно (отрицательно) определенной тогда и только тогда, когда все собственные значения ее матрицы положительны (отрицательны).

Теорема (критерий Сильвестра). Квадратичная форма является положительно определенной тогда и только тогда, когда все главные миноры матрицы этой формы положительны.

Главным (угловым) минором k-го порядка матрицы А n-го порядка называют определитель матрицы, составленный из первых k строк и столбцов матрицы А ().

Отметим, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, причем минор первого порядка должен быть отрицательным.

Например, исследуем на знакоопределенность квадратичную форму f(х 1 , х 2) = 2x 1 2 + 4х 1 х 2 + 3х 2 2 .

= (2 - l)*
*(3 - l) - 4 = (6 - 2l - 3l + l 2) - 4 = l 2 - 5l + 2 = 0; D = 25 - 8 = 17;
. Следовательно, квадратичная форма - положительно определенная.

Способ 2. Главный минор первого порядка матрицы А D 1 = a 11 = 2 > 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 > 0. Следовательно, по критерию Сильвестра квадратичная форма - положительно определенная.

Исследуем на знакоопределенность другую квадратичную форму, f(х 1 , х 2) = -2x 1 2 + 4х 1 х 2 - 3х 2 2 .

Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид = (-2 - l)*
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17;
. Следовательно, квадратичная форма - отрицательно определенная.

Способ 2. Главный минор первого порядка матрицы А D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 > 0. Следовательно, по критерию Сильвестра квадратичная форма - отрицательно определенная (знаки главных миноров чередуются, начиная с минуса).

И в качестве еще одного примера исследуем на знакоопределенность квадратичную форму f(х 1 , х 2) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 .

Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид = (2 - l)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41;
.

Одно из этих чисел отрицательно, а другое - положительно. Знаки собственных значений разные. Следовательно, квадратичная форма не может быть ни отрицательно, ни положительно определенной, т.е. эта квадратичная форма не является знакоопределенной (может принимать значения любого знака).

Способ 2. Главный минор первого порядка матрицы А D 1 = a 11 = 2 > 0. Главный минор второго порядка D 2 = = -6 - 4 = -10 < 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

СИСТЕМА ОДНОРОДНЫХ ЛИНЕЙНЫХ УРАВНЕНИЙ

Системой однородных линейных уравнений называется система вида

Ясно, что в этой случае , т.к. все элементы одного из столбцов в этих определителях равны нулю.

Так как неизвестные находятся по формулам , то в случае, когда Δ ≠ 0, система имеет единственное нулевое решение x = y = z = 0. Однако, во многих задачах интересен вопрос о том, имеет ли однородная система решения отличные от нулевого.

Теорема. Для того, чтобы система линейных однородных уравнений имела ненулевое решение, необходимо и достаточно, чтобы Δ ≠ 0.

Итак, если определитель Δ ≠ 0, то система имеет единственное решение. Если же Δ ≠ 0, то система линейных однородных уравнений имеет бесконечное множество решений.

Примеры.

СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ

Пусть задана квадратная матрица , X – некоторая матрица–столбец, высота которой совпадает с порядком матрицы A . .

Во многих задачах приходится рассматривать уравнение относительно X

где λ – некоторое число. Понятно, что при любом λ это уравнение имеет нулевое решение .

Число λ, при котором это уравнение имеет ненулевые решения, называется собственным значением матрицы A , а X при таком λ называется собственным вектором матрицы A .

Найдём собственный вектор матрицы A . Поскольку E ∙X = X , то матричное уравнение можно переписать в виде или . В развёрнутом виде это уравнение можно переписать в виде системы линейных уравнений. Действительно .

И, следовательно,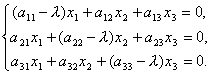

Итак, получили систему однородных линейных уравнений для определения координат x 1 , x 2 , x 3 вектора X . Чтобы система имела ненулевые решения необходимо и достаточно, чтобы определитель системы был равен нулю, т.е.

Это уравнение 3-ей степени относительно λ. Оно называется характеристическим уравнением матрицы A и служит для определения собственных значений λ.

Каждому собственному значению λ соответствует собственный вектор X , координаты которого определяются из системы при соответствующем значении λ.

Примеры.

ВЕКТОРНАЯ АЛГЕБРА. ПОНЯТИЕ ВЕКТРОРА

При изучении различных разделов физики встречаются величины, которые полностью определяются заданием их численных значений, например, длина, площадь, масса, температура и т.д. Такие величины называются скалярными. Однако, кроме них встречаются и величины, для определения которых, кроме численного значения, необходимо знать также их направление в пространстве, например, сила, действующая на тело, скорость и ускорение тела при его движении в пространстве, напряжённость магнитного поля в данной точке пространства и т.д. Такие величины называются векторными.

Введём строгое определение.

Направленным отрезком назовём отрезок, относительно концов которого известно, какой из них первый, а какой второй.

Вектором называется направленный отрезок, имеющий определённую длину, т.е. это отрезок определённой длины, у которого одна из ограничивающих его точек принимается за начало, а вторая – за конец. Если A – начало вектора, B – его конец, то вектор обозначается символом, кроме того, вектор часто обозначается одной буквой . На рисунке вектор обозначается отрезком, а его направление стрелкой.

Модулем или длиной вектора называют длину определяющего его направленного отрезка. Обозначается || или ||.

К векторам будем относить и так называемый нулевой вектор, у которого начало и конец совпадают. Он обозначается . Нулевой вектор не имеет определенного направления и модуль его равен нулю ||=0.

Векторы и называются коллинеарными , если они расположены на одной прямой или на параллельных прямых. При этом если векторы и одинаково направлены, будем писать , противоположно .

Векторы, расположенные на прямых, параллельных одной и той же плоскости, называются компланарными .

Два вектора и называются равными , если они коллинеарны, одинаково направлены и равны по длине. В этом случае пишут .

Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, помещая его начало в любую точку пространства.

Например .

ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ

1. Умножение вектора на число.

   Произведением вектора на число λ называется новый вектор такой, что:

   Произведение вектора на число λ обозначается .

   

   Например, есть вектор, направленный в ту же сторону, что и вектор , и имеющий длину, вдвое меньшую, чем вектор .

   Введённая операция обладает следующими свойствами :

2. Сложение векторов.

   Пусть и – два произвольных вектора. Возьмём произвольную точку O и построим вектор . После этого из точки A отложим вектор . Вектор , соединяющий начало первого вектора c концом второго , называется суммой этих векторов и обозначается .

   

   Сформулированное определение сложения векторов называют правилом параллелограмма , так как ту же самую сумму векторов можно получить следующим образом. Отложим от точки O векторы и . Построим на этих векторах параллелограмм ОАВС . Так как векторы , то вектор , являющийся диагональю параллелограмма, проведённой из вершины O , будет очевидно суммой векторов .

   

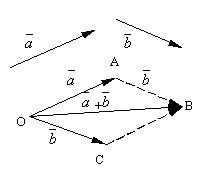
   Легко проверить следующие свойства сложения векторов .

3. Разность векторов.

   Вектор, коллинеарный данному вектору , равный ему по длине и противоположно направленный, называется противоположным вектором для вектора и обозначается . Противоположный вектор можно рассматривать как результат умножения вектора на число λ = –1: .