Найти острый угол между прямыми онлайн. Угол между прямыми на плоскости

а. Пусть даны две прямые Эти прямые как было указано в главе 1, образуют различные положительные и отрицательные углы, которые при этом могут быть как острыми, так и тупыми. Зная один из этих углов мы легко найдем какой-либо другой.

Между прочим, у всех этих углов численная величина тангенса одна и та же, различие может быть только в знаке

Уравнения прямых. Числа суть проекции направляющих векторов первой и второй прямой Угол между этими векторами равен одному из углов, образуемых прямыми линиями. Поэтому задача сводится к определению угла между векторами, Мы получим

Для простоты можно условиться под углом между двумя прямыми понимать острый положительный угол (как, например, на рис. 53).

Тогда тангенс этого угла будет всегда положительным. Таким образом, если в правой части формулы (1) получится знак минус, то мы его должны отбросить, т. е. сохранить только абсолютную величину.

Пример. Определить угол между прямыми

По формуле (1) имеем

с. Если будет указано, какая из сторон угла является его началом и какая концом, то, отсчитывая всегда направление угла против часовой стрелки, мы можем формулы (1) извлечь нечто большее. Как нетрудно убедиться из рис. 53 знак получающийся в правой части формулы (1), будет указывать, какой именно - острый или тупой - угол образует вторая прямая с первой.

(Действительно, из рис, 53 мы усматриваем, что угол между первым и вторым направляющими векторами или равен искомому углу между прямыми, или отличается от него на ±180°.)

d. Если прямые параллельны, то параллельны и их направляющие векторы, Применяя условие параллельности двух векторов получим!

Это есть условием необходимое и достаточное для параллельности двух прямых.

Пример. Прямые

параллельны, так как

e. Если прямые перпендикулярны то их направляющие векторы тоже перпендикулярны. Применяя условие перпендикулярности двух векторов мы получим условие перпендикулярности двух прямых а именно

Пример. Прямые

перпендикулярны ввиду того, что

В связи с условиями параллельности и перпендикулярности решим следующие две задачи.

f. Через точку провести прямую параллельно данной прямой

Решение проводится так. Так как искомая прямая параллельна данной, то за ее направляющий вектор можно взять тот же самый, что и у данной прямой, т. е. вектор с проекциями А и В. А тогда уравнение искомой прямой напишется в форме (§ 1)

Пример. Уравнение прямой, проходящей через точку (1; 3) параллельно прямой

будет следующее!

g. Через точку провести прямую перпендикулярно данной прямой

Здесь за направляющий вектор уже не годится брать вектор с проекциями А и , а надо веять вектор, ему перпендикулярный. Проекции этого вектора должны быть выбраны следовательно, согласно условию перпендикулярности обоих векторов, т. е. согласно условию

Выполнить же это условие можно бесчисленным множеством способов, так как здесь одно уравнение с двумя неизвестными Но проще всего взять иди же Тогда уравнение искомой прямой напишется в форме

Пример. Уравнение прямой, проходящей через точку (-7; 2) в перпендикулярной прямой

будет следующее (по второй формуле)!

h. В том случаем когда прямые заданы уравнениями вида

УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Рассмотрим две плоскости α 1 и α 2 , заданные соответственно уравнениями:

Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α 1 и α 2 равен одному из указанных смежных двугранных углов или . Поэтому . Т.к. и , то

Пример. Определить угол между плоскостями x +2y -3z +4=0 и 2x +3y +z +8=0.

Условие параллельности двух плоскостей.

Две плоскости α 1 и α 2 параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит .

Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

или

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .

Таким образом, .

Примеры.

ПРЯМАЯ В ПРОСТРАНСТВЕ.

ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ.

ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

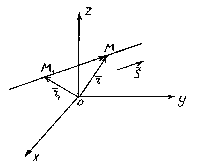
Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М 1 и вектора , параллельного этой прямой.

Вектор , параллельный прямой, называется направляющим вектором этой прямой.

Итак, пусть прямая l проходит через точку М 1 (x 1 , y 1 , z 1), лежащую на прямой параллельно вектору .

Рассмотрим произвольную точку М(x,y,z) на прямой. Из рисунка видно, что .

Векторы и коллинеарны, поэтому найдётся такое число t , что , где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М 1 и М соответственно через и , получаем . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М , лежащей на прямой.

Запишем это уравнение в координатной форме. Заметим, что , и отсюда

Полученные уравнения называются параметрическими уравнениями прямой.

При изменении параметра t изменяются координаты x , y и z и точка М перемещается по прямой.

КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

Пусть М 1 (x 1 , y 1 , z 1) – точка, лежащая на прямой l , и – её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z) и рассмотрим вектор .

Ясно, что векторы и коллинеарные, поэтому их соответствующие координаты должны быть пропорциональны, следовательно,

– канонические уравнения прямой.

Замечание 1. Заметим, что канонические уравнения прямой можно было получить из параметрических,исключив параметр t . Действительно, из параметрических уравнений получаем или .

Пример. Записать уравнение прямой в параметрическом виде.

Обозначим , отсюда x = 2 + 3t , y = –1 + 2t , z = 1 –t .

Замечание 2. Пусть прямая перпендикулярна одной из координатных осей, например оси Ox . Тогда направляющий вектор прямой перпендикулярен Ox , следовательно, m =0. Следовательно, параметрические уравнения прямой примут вид

Исключая из уравнений параметр t , получим уравнения прямой в виде

Однако и в этом случае условимся формально записывать канонические уравнения прямой в виде. Таким образом, еслив знаменателе одной из дробей стоит нуль, то это означает, что прямая перпендикулярна соответствующей координатной оси.

Аналогично, каноническим уравнениям соответствует прямая перпендикулярная осям Ox и Oy или параллельная оси Oz .

Примеры.

ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ

Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.

Вообще любые две не параллельные плоскости, заданные общими уравнениями

определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.

Примеры.

Построить прямую, заданную уравнениями

Для построения прямой достаточно найти любые две ее точки. Проще всего выбрать точки пересечения прямой с координатными плоскостями. Например, точку пересечения с плоскостью xOy получим из уравнений прямой, полагая z = 0:

Решив эту систему, найдем точку M 1 (1;2;0).

Аналогично, полагая y = 0, получим точку пересечения прямой с плоскостью xOz :

От общих уравнений прямой можно перейтик её каноническим или параметрическим уравнениям. Для этого нужно найти какую-либо точку М 1 на прямой и направляющий вектор прямой.

Координаты точки М 1 получим из данной системы уравнений, придав одной из координат произвольное значение. Для отыскания направляющего вектора, заметим, что этот вектор должен быть перпендикулярен к обоим нормальным векторам и . Поэтому за направляющий вектор прямой l можно взять векторное произведение нормальных векторов:

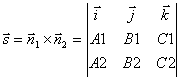Пример. Привести общие уравнения прямой к каноническому виду.

Найдём точку, лежащую на прямой. Для этого выберем произвольно одну из координат, например, y = 0 и решим систему уравнений:

Нормальные векторы плоскостей, определяющих прямую имеют координаты Поэтому направляющий вектор прямой будет

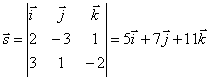. Следовательно, l : .

УГОЛ МЕЖДУ ПРЯМЫМИ

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим

Пусть две прямые l и m на плоскости в декартовой системе координат заданы общими уравнениями: l: A 1 x + B 1 y + C 1 = 0, m: A 2 x + B 2 y + C 2 = 0

Векторы нормалей к данным прямым: = (A 1 , B 1) – к прямой l,

= (A 2 , B 2) – к прямой m.

Пусть j - угол между прямыми l и m.

Так как углы с взаимно перпендикулярными сторонами либо равны, либо в сумме составляют p, то , то есть cos j = .

Итак, мы доказали следующую теорему.

Теорема. Пусть j - угол между двумя прямыми на плоскости, и пусть эти прямые заданы в декартовой системе координат общими уравнениями A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0. Тогда cos j = .

Упражнения.

1) Выведите формулу для вычисления угла между прямыми, если:

(1) обе прямые заданы параметрически; (2) обе прямые заданы каноническими уравнениями; (3) одна прямая задана параметрически, другая прямая – общим уравнением; (4) обе прямые заданы уравнением с угловым коэффициентом.

2) Пусть j - угол между двумя прямыми на плоскости, и пусть эти прямые заданы декартовой системе координат уравнениями y = k 1 x + b 1 и y =k 2 x + b 2 .

Тогда tg j = .

3) Исследуйте взаимное расположение двух прямых, заданных общими уравнениями в декартовой системе координат, и заполните таблицу:

Расстояние от точки до прямой на плоскости.

Пусть на плоскости в декартовой системе координат прямая l задана общим уравнением Ax + By + C = 0. Найдем расстояние от точки M(x 0 , y 0) до прямой l.

Расстояние от точки M до прямой l – это длина перпендикуляра HM (H Î l, HM ^ l).

Вектор и вектор нормали к прямой l коллинеарны, так что | | = | | | | и | | = .

Пусть координаты точки H (x,y).

Так как точка H принадлежит прямой l, то Ax + By + C = 0 (*).

Координаты векторов и : = (x 0 - x, y 0 - y), = (A, B).

| | = = =

(C = -Ax - By , см. (*))

Теорема. Пусть прямая l задана в декартовой системе координат общим уравнением Ax + By + C = 0. Тогда расстояние от точки M(x 0 , y 0) до данной прямой вычисляется по формуле: r (M; l) = .

Упражнения.

1) Выведите формулу для вычисления расстояния от точки до прямой, если: (1) прямая задана параметрически; (2) прямая задана каноническим уравнениям; (3) прямая задана уравнением с угловым коэффициентом.

2) Напишите уравнение окружности, касающейся прямой 3x – y = 0,с центром в точке Q(-2,4).

3) Напишите уравнения прямых, делящих углы, образованные пересечением прямых 2x + y - 1 = 0 и x + y + 1 = 0 , пополам.

§ 27. Аналитическое задание плоскости в пространстве

Определение . Вектором нормали к плоскости будем называть ненулевой вектор, любой представитель которого перпендикулярен данной плоскости.

Замечание. Ясно, что если хотя бы один представитель вектора перпендикулярен плоскости, то и все остальные представители вектора перпендикулярны этой плоскости.

Пусть в пространстве задана декартова система координат.

Пусть дана плоскость a, = (A, B, C) – вектор нормали к этой плоскости, точка M (x 0 , y 0 , z 0) принадлежит плоскости a.

Для любой точки N(x, y, z) плоскости a векторы и ортогональны, то есть их скалярное произведение равно нулю: = 0. Запишем последнее равенство в координатах: A(x - x 0) + B(y - y 0) + C(z - z 0) = 0.

Пусть -Ax 0 - By 0 - Cz 0 = D, тогда Ax + By + Cz + D = 0.

Возьмем точку К (x, y) такую, что Ax + By + Cz + D = 0. Так как D = -Ax 0 - By 0 - Cz 0 , то A(x - x 0) + B(y - y 0) + C(z - z 0) = 0. Так как координаты направленного отрезка = (x - x 0 , y - y 0 , z - z 0), то последнее равенство означает, что ^ , и, следовательно, K Î a.

Итак, мы доказали следующую теорему:

Теорема. Любую плоскость в пространстве в декартовой системе координат можно задать уравнением вида Ax + By + Cz + D = 0 (A 2 + B 2 + C 2 ≠ 0), где (A, B, C) – координаты вектора нормали к этой плоскости.

Верно и обратное.

Теорема. Любое уравнение вида Ax + By + Cz + D = 0 (A 2 + B 2 + C 2 ≠ 0) в декартовой системе координат задает некоторую плоскость, при этом (A, B, C) – координаты вектора нормали к этой плоскости.

Доказательство.

Возьмем точку M (x 0 , y 0 , z 0) такую, что Ax 0 + By 0 + Cz 0 + D = 0 и вектор = (A, B, C) ( ≠ q).

Через точку M перпендикулярно вектору проходит плоскость (и при том только одна). По предыдущей теореме эта плоскость задается уравнением Ax + By + Cz + D = 0.

Определение. Уравнение вида Ax + By + Cz + D = 0 (A 2 + B 2 + C 2 ≠ 0) называется общим уравнением плоскости .

Пример.

Напишем уравнение плоскости, проходящей через точки M (0,2,4), N (1,-1,0) и K (-1,0,5).

1. Найдем координаты вектора нормали к плоскости (MNK). Так как векторное произведение ´ ортогонально не коллинеарным векторам и , то вектор коллинеарен ´ .

= (1, -3, -4), = (-1, -2, 1);

´ = ,

´ = (-11, 3, -5).

Итак, в качестве вектора нормали возьмем вектор = (-11, 3, -5).

2. Воспользуемся теперь результатами первой теоремы:

уравнение данной плоскости A(x - x 0) + B(y - y 0) + C(z - z 0) = 0, где (A, B, C) – координаты вектора нормали, (x 0 , y 0 , z 0) – координаты точки лежащей в плоскости (например, точки M).

11(x - 0) + 3(y - 2) - 5(z - 4) = 0

11x + 3y – 5z + 14 = 0

Ответ: -11x + 3y - 5z + 14 = 0.

Упражнения.

1) Напишите уравнение плоскости, если

(1) плоскость проходит через точку M (-2,3,0) параллельно плоскости 3x + y + z = 0;

(2) плоскость содержит ось (Ox) и перпендикулярна плоскости x + 2y – 5z + 7 = 0.

2) Напишите уравнение плоскости, проходящей через три данные точки.

§ 28. Аналитическое задание полупространства*

Замечание* . Пусть фиксирована некоторая плоскость. Под полупространством мы будем понимать множество точек, лежащих по одну сторону от данной плоскости, то есть две точки лежат в одном полупространстве, если отрезок, их соединяющий, не пересекает данную плоскость. Данная плоскость называется границей этого полупространства . Объединение данной плоскости и полупространства будем называть замкнутым полупространством .

Пусть в пространстве фиксирована декартова система координат.

Теорема. Пусть плоскость a задана общим уравнением Ax + By + Cz + D = 0. Тогда одно из двух полупространств, на которые плоскость a делит пространство, задается неравенством Ax + By + Cz + D > 0, а второе полупространство задается неравенством Ax + By + Cz + D < 0.

Доказательство.

Отложим вектор нормали = (A, B, С) к плоскости a от точки M (x 0 , y 0 , z 0), лежащей на данной плоскости: = , M Î a, MN ^ a. Плоскость делить пространство на два полупространства: b 1 и b 2 . Ясно, что точка N принадлежит одному из этих полупространств. Без ограничения общности будем считать, что N Î b 1 .

Докажем, что полупространство b 1 задается неравенством Ax + By + Cz + D > 0.

1) Возьмем точку K(x,y,z) в полупространстве b 1 . Угол Ð NMK – угол между векторами и - острый, поэтому скалярное произведение этих векторов положительно: > 0. Запишем это неравенство в координатах: A(x - x 0) + B(y - y 0) + C(z - z 0) > 0, то есть Ax + By + Cy - Ax 0 - By 0 - C z 0 > 0.

Так как M Î b 1 , то Ax 0 + By 0 + C z 0 + D = 0, поэтому -Ax 0 - By 0 - C z 0 = D. Следовательно, последнее неравенство можно записать так: Ax + By + Cz + D > 0.

2) Возьмем точку L(x,y) такую, что Ax + By + Cz + D > 0.

Перепишем неравенство, заменив D на (-Ax 0 - By 0 - C z 0) (так как M Î b 1 , то Ax 0 + By 0 + C z 0 + D = 0): A(x - x 0) + B(y - y 0) + C(z - z 0) > 0.

Вектор с координатами (x - x 0 ,y - y 0 , z - z 0) – это вектор , поэтому выражение A(x - x 0) + B(y - y 0) + C(z - z 0) можно понимать, как скалярное произведение векторов и . Так как скалярное произведение векторов и положительно, то угол между ними острый и точка L Î b 1 .

Аналогично можно доказать, что полупространство b 2 задается неравенством Ax + By + Cz + D < 0.

Замечания.

1) Ясно, что доказательство, приведенное выше, не зависит от выбора точки M в плоскости a.

2) Ясно, что одно и то же полупространство можно задать различными неравенствами.

Верно и обратное.

Теорема. Любое линейное неравенство вида Ax + By + Cz + D > 0 (или Ax + By + Cz + D < 0) (A 2 + B 2 + C 2 ≠ 0) задает в пространстве в декартовой системе координат полупространство с границей Ax + By + Cz + D = 0.

Доказательство.

Уравнение Ax + By + Cz + D = 0 (A 2 + B 2 + C 2 ≠ 0) в пространстве задает некоторую плоскость a (см. § …). Как было доказано в предыдущей теореме одно из двух полупространств, на которые плоскость делит пространство задается неравенством Ax Ax + By + Cz + D > 0.

Замечания.

1) Ясно, что замкнутое полупространство можно задать нестрогим линейным неравенством, и любое нестрогое линейное неравенство в декартовой системе координат задает замкнутое полупространство.

2) Любой выпуклый многогранник можно задать как пересечение замкнутых полупространств (границы которых – это плоскости, содержащие грани многогранника), то есть аналитически – системой линейных нестрогих неравенств.

Упражнения.

1) Докажите две представленные теоремы для произвольной аффинной системы координат.

2) Верно ли обратное, что любая ли система нестрогих линейных неравенств задает выпуклый многоугольник?

Упражнение.

1) Исследуйте взаимное расположение двух плоскостей, заданных общими уравнениями в декартовой системе координат, и заполните таблицу.

Пусть в пространстве заданы две прямые:

Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов и :

Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l 1 параллельна l 2 тогда и только тогда, когда параллелен .

Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю: .

Угол между прямой и плоскостью

Пусть прямая d - не перпендикулярна плоскости θ;
d ′− проекция прямой d на плоскость θ;
Наименьший из углов между прямыми d и d ′ мы назовем углом между прямой и плоскостью .
Обозначим его как φ=(d ,θ)
Если d ⊥θ , то (d ,θ)=π/2

Oi →j →k →− прямоугольная система координат.
Уравнение плоскости:

θ:Ax +By +Cz +D =0

Считаем, что прямая задана точкой и направляющим вектором: d [M 0,p →]
Вектор n →(A ,B ,C )⊥θ
Тогда остается выяснить угол между векторами n → и p →, обозначим его как γ=(n →,p →).

Если угол γ<π/2 , то искомый угол φ=π/2−γ .

Если угол γ>π/2 , то искомый угол φ=γ−π/2

sinφ=sin(2π−γ)=cosγ

sinφ=sin(γ−2π)=−cosγ

Тогда, угол между прямой и плоскостью можно считать по формуле:

sinφ=∣cosγ∣=∣ ∣ Ap 1+Bp 2+Cp 3∣ ∣ √A 2+B 2+C 2√p 21+p 22+p 23

Вопрос29. Понятие квадратичной формы. Знакоопределенность квадратичных форм.

Квадратичной формой j (х 1 , х 2 , …, x n) n действительных переменных х 1 , х 2 , …, x n называется сумма вида
, (1)

где a ij – некоторые числа, называемые коэффициентами. Не ограничивая общности, можно считать, что a ij = a ji .

Квадратичная форма называется действительной, если a ij Î ГR. Матрицей квадратичной формы называется матрица, составленная из ее коэффициентов. Квадратичной форме (1) соответствует единственная симметричная матрица
Т. е. А Т = А . Следовательно, квадратичная форма (1) может быть записана в матричном виде j (х ) = х Т Ах , где х Т = (х 1 х 2 … x n ). (2)

И, наоборот, всякой симметричной матрице (2) соответствует единственная квадратичная форма с точностью до обозначения переменных.

Рангом квадратичной формы называют ранг ее матрицы. Квадратичная форма называется невырожденной, если невырожденной является ее матрица А . (напомним, что матрица А называется невырожденной, если ее определитель не равен нулю). В противном случае квадратичная форма является вырожденной.

положительно определенной (или строго положительной), если

j (х ) > 0 , для любого х = (х 1 , х 2 , …, x n ), кроме х = (0, 0, …, 0).

Матрица А положительно определенной квадратичной формы j (х ) также называется положительно определенной. Следовательно, положительно определенной квадратичной форме соответствует единственная положительно определенная матрица и наоборот.

Квадратичная форма (1) называется отрицательно определенной (или строго отрицательной), если

j (х ) < 0, для любого х = (х 1 , х 2 , …, x n ), кроме х = (0, 0, …, 0).

Аналогично как и выше, матрица отрицательно определенной квад-ратичной формы также называется отрицательно определенной.

Следовательно, положительно (отрицательно) определенная квадра-тичная форма j (х ) достигает минимального (максимального) значения j (х* ) = 0 при х* = (0, 0, …, 0).

Отметим, что большая часть квадратичных форм не является знакоопределенными, то есть они не являются ни положительными, ни отрицательными. Такие квадратичные формы обращаются в 0 не только в начале системы координат, но и в других точках.

Когда n > 2 требуются специальные критерии для проверки знакоопределенности квадратичной формы. Рассмотрим их.

Главными минорами квадратичной формы называются миноры:

то есть это миноры порядка 1, 2, …, n матрицы А , расположенные в левом верхнем углу, последний из них совпадает с определителем матрицы А .

Критерий положительной определенности (критерий Сильвестра)

х ) = х Т Ах была положительно определенной, необходимо и достаточно, что все главные миноры матрицы А были положительны, то есть: М 1 > 0, M 2 > 0, …, M n > 0. Критерий отрицательной определенности Для того чтобы квадратичная форма j (х ) = х Т Ах была отрицательно определенной, необходимо и достаточно, чтобы ее главные миноры четного порядка были положительны, а нечетного – отрицательны, т. е.: М 1 < 0, M 2 > 0, М 3 < 0, …, (–1) n

Определение. Если заданы две прямые y = k 1 x + b 1 , y = k 2 x + b 2 , то острый угол между этими прямыми будет определяться как

Две прямые параллельны, если k 1 = k 2 . Две прямые перпендикулярны, если k 1 = -1/ k 2 .

Теорема. Прямые Ах + Ву + С = 0 и А 1 х + В 1 у + С 1 = 0 параллельны, когда пропорциональны коэффициенты А 1 = λА, В 1 = λВ. Если еще и С 1 = λС, то прямые совпадают. Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.

Уравнение прямой, проходящей через данную точку

Перпендикулярно данной прямой

Определение. Прямая, проходящая через точку М 1 (х 1 , у 1) и перпендикулярная к прямой у = kx + b представляется уравнением:

Расстояние от точки до прямой

Теорема. Если задана точка М(х 0 , у 0), то расстояние до прямой Ах + Ву + С =0 определяется как

Доказательство. Пусть точка М 1 (х 1 , у 1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М 1:

(1)

Координаты x 1 и у 1 могут быть найдены как решение системы уравнений:

Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М 0 перпендикулярно заданной прямой. Если преобразовать первое уравнение системы к виду:

A(x – x 0) + B(y – y 0) + Ax 0 + By 0 + C = 0,

то, решая, получим:

Подставляя эти выражения в уравнение (1), находим:

Теорема доказана.

Пример . Определить угол между прямыми: y = -3 x + 7; y = 2 x + 1.

k 1 = -3; k 2 = 2; tgφ = ; φ= p /4.

Пример . Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.

Решение . Находим: k 1 = 3/5, k 2 = -5/3, k 1* k 2 = -1, следовательно, прямые перпендикулярны.

Пример . Даны вершины треугольника А(0; 1), B (6; 5), C (12; -1). Найти уравнение высоты, проведенной из вершины С.

Решение . Находим уравнение стороны АВ: ; 4 x = 6 y – 6;

2 x – 3 y + 3 = 0;

Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b . k = . Тогда y = . Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: откуда b = 17. Итого: .

Ответ: 3 x + 2 y – 34 = 0.

Уравнение прямой, проходящей через данную точку в данном направлении. Уравнение прямой, проходящей через две данные точки. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых. Определение точки пересечения двух прямых

1. Уравнение прямой, проходящей через данную точку A (x 1 , y 1) в данном направлении, определяемом угловым коэффициентом k ,

y - y 1 = k (x - x 1). (1)

Это уравнение определяет пучок прямых, проходящих через точку A (x 1 , y 1), которая называется центром пучка.

2. Уравнение прямой, проходящей через две точки: A (x 1 , y 1) и B (x 2 , y 2), записывается так:

Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле

3. Углом между прямыми A и B называется угол, на который надо повернуть первую прямую A вокруг точки пересечения этих прямых против движения часовой стрелки до совпадения ее со второй прямой B . Если две прямые заданы уравнениями с угловым коэффициентом

y = k 1 x + B 1 ,

y = k 2 x + B 2 , (4)

то угол между ними определяется по формуле

Следует обратить внимание на то, что в числителе дроби из углового коэффициента второй прямой вычитается угловой коэффициент первой прямой.

Если уравнения прямой заданы в общем виде

A 1 x + B 1 y + C 1 = 0,

A 2 x + B 2 y + C 2 = 0, (6)

угол между ними определяется по формуле

4. Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k 1 = k 2 . (8)

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

5. Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

Это условие может быть записано также в виде

k 1 k 2 = -1. (11)

б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства

A 1 A 2 + B 1 B 2 = 0. (12)

6. Координаты точки пересечения двух прямых находят, решая систему уравнений (6). Прямые (6) пересекаются в том и только в том случае, когда

1. Напишите уравнения прямых, проходящих через точку M, одна из которых параллельна, а другая – перпендикулярна заданной прямой l.